Tài liệu Giáo viên
Lớp 2Lớp 2 - kết nối tri thức
Lớp 2 - Chân trời sáng sủa tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - liên kết tri thức
Lớp 3 - Chân trời sáng tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Tài liệu Giáo viên
Lớp 4Lớp 4 - kết nối tri thức
Lớp 4 - Chân trời sáng tạo
Lớp 4 - Cánh diều
Tiếng Anh lớp 4
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - kết nối tri thức
Lớp 6 - Chân trời sáng tạo
Lớp 6 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 7Lớp 7 - liên kết tri thức
Lớp 7 - Chân trời sáng sủa tạo
Lớp 7 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 8Lớp 8 - kết nối tri thức
Lớp 8 - Chân trời sáng sủa tạo
Lớp 8 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - kết nối tri thức
Lớp 10 - Chân trời sáng sủa tạo
Lớp 10 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 11Lớp 11 - liên kết tri thức
Lớp 11 - Chân trời sáng tạo
Lớp 11 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
thầy giáoLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Chuyên đề Toán 9Chuyên đề: Hệ hai phương trình bậc nhất hai ẩn
Chuyên đề: Phương trình bậc hai một ẩn số
Chuyên đề: Hệ thức lượng vào tam giác vuông
Chuyên đề: Đường tròn
Chuyên đề: Góc với mặt đường tròn
Chuyên đề: hình tròn - Hình Nón - Hình Cầu
Đồ thị hàm số y= ax + b (a ≠ 0)
Trang trước
Trang sau
Đồ thị hàm số y= ax + b (a ≠ 0)
A. Phương pháp giải
Phương pháp
1, Đường thẳng y=ax+b có hệ số góc là a.
Bạn đang xem: Đồ thị hàm số bậc nhất
2, hai đường thẳng song song thì có thông số góc bởi nhau
3, hai đường thẳng vuông góc thì bao gồm tích hệ số góc bởi -1
4, Đường thẳng y=ax+b(a > 0) sinh sản với tia Ox một góc thì
5, biện pháp vẽ vật dụng thị hàm số y=ax+b ( a ≠ 0).
1, Xét trường phù hợp b=0
Khi b=0 thì y=a.x. Đồ thị của hàm số y= ax là mặt đường thẳng đi qua gốc tọa độ O(0; 0) cùng điểm A(1; a).
2, Xét trường thích hợp y=ax+b cùng với
Bước 1: cho x=0 thì y=b, ta được điểm P(0;b) trực thuộc trục Oy.
Cho y= 0 thì x= -b/a , ta đạt điểm Q(-b/a;0) trực thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng trải qua hai điểm p và Q ta được đồ gia dụng thị hàm số y=ax+b.
B. Bài bác tập tự luận
Bài 1: Vẽ thiết bị thị hàm số của những hàm số a, y= 2xb, y=-3x+3
Hướng dẫn giải
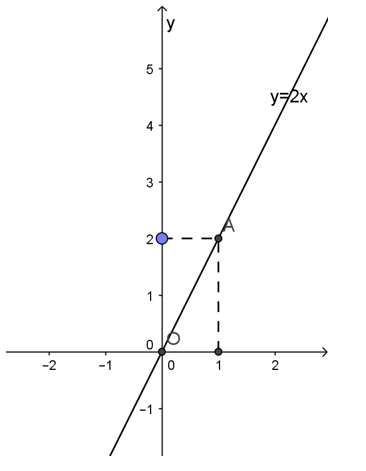
a, y=2x
Đồ thị hàm số y=2x trải qua điểm O(0; 0) với điểm A(1; 2)
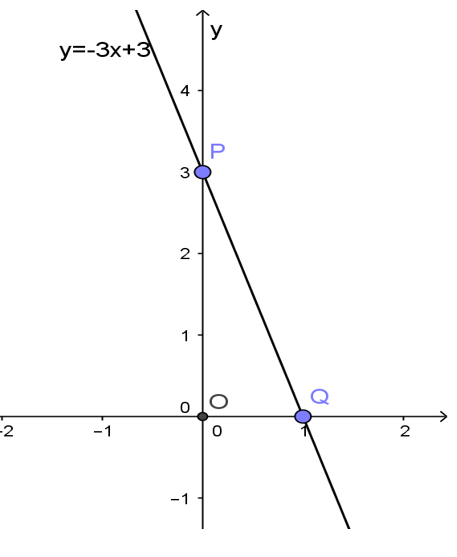
b, y=-3x+3
Cho x=0 thì y=3, ta lấy điểm P(0; 3) nằm trong trục tung Oy
Cho y=0 thì x=1, ta lấy điểm Q(1; 0) trực thuộc trục hoành Ox
Vẽ con đường thẳng trải qua hai điểm p và Q ta được đồ dùng thị hàm số y=-3x+3
Bài 2: a, mang lại đồ thị hàm số y=ax+7 đi qua M(2; 11). Search a
b, hiểu được khi x=3 thì hàm số y=2x+b có mức giá trị bởi 8, tra cứu b
c, cho hàm số y=(m+1)x. Xác minh m để đồ thị hàm số đi qua A(1; 2)
Hướng dẫn giải
a, bởi đồ thị hàm số y=ax+7 (1) trải qua M(2; 11) buộc phải thay x=2; y=11 vào (1) ta được:11=2a+7. Từ kia suy ra a=2.
Vậy a=2
b, nạm y=8; x=3 vào hàm số y=2x+b ta được: 8=6+b. Suy ra b=2
Vậy b=2
c, bởi đồ thị hàm số y=(m+1)x (2) đi qua A(1; 2) buộc phải thay x=1; y=2 vào (2) ta được: 2=(m+1).1. Từ kia suy ra m=1
Vậy m=1
Bài 3: xác minh hàm số y=ax+b trong những trường hòa hợp sau, biết thiết bị thị của hàm số là con đường thẳng đi qua gốc tọa độ và:a, Đi qua điểm A(3;2)
b, Có hệ số a= √3
c, tuy vậy song với mặt đường thẳng y=3x+1
Hướng dẫn giải
Nhắc lại: Đồ thị hàm số trải qua gốc tọa độ O(0;0) có dạng y=ax (a ≠0)
a, do đồ thị hàm số y=ax+b (a ≠ 0) đi qua gốc tọa độ O(0;0) nên có dạng y=ax (a ≠ 0)
Vì vật dụng thị hàm số đi qua điểm A(3;2) đề xuất ta có: 2=3.a &h
Arr; a = 2/3
Vậy hàm số yêu cầu tìm là y = 2/3x
b, vì chưng đồ thị hàm số y=ax+b (a ≠ 0) trải qua gốc tọa độ O(0;0) nên bao gồm dạng y=ax(a ≠ 0)
Vì hàm số đã mang lại có hệ số góc là a= √3 buộc phải hàm số đề xuất tìm là y= √3x
c, bởi vì đồ thị hàm số y=ax+b (a ≠ 0) đi qua gốc tọa độ O(0;0) nên bao gồm dạng y=ax( a ≠ 0)
Vì đồ vật thị hàm số y=ax (a ≠ 0) tuy vậy song với đường thẳng y=3x+1 yêu cầu a=3.
Vậy hàm số yêu cầu tìm là y=3x.
Bài 4: cho đường thẳng y=(k+1)x+k. (1)
a, Tìm cực hiếm của k để mặt đường thẳng (1) trải qua gốc tọa độ.
b, Tìm cực hiếm của k để con đường thẳng (1) cắt trục tung trên điểm bao gồm tung độ bằng 2.
c, Tìm cực hiếm của k để đường thẳng (1) tuy vậy song với đường thẳng y=5x-5.
Hướng dẫn giải
a, Đường thẳng y=ax+b đi qua gốc tọa độ khi b=0, đề nghị đường thẳng y=(k+1)x+k qua nơi bắt đầu tọa độ lúc k=0, lúc đó hàm số là y=x.
b, Đường thẳng y=ax+b giảm trục tung trên điểm có tung độ bằng b. Vì chưng đó, mặt đường thẳng y=(k+1)x+k cắt trục tung trên điểm bao gồm tung độ bằng 2 lúc k=2.
Vậy k=2 và mặt đường thẳng yêu cầu tìm là y=3x+2
c, Đường thẳng y=(k+1)x+k tuy nhiên song với con đường thẳng y=5x-5 khi còn chỉ khi k+1=5 và. Từ đó suy ra k=4.
Vậy hàm số đề xuất tìm là y=5x+4.
Bài 5: a, Vẽ đồ vật thị của các hàm số y=x+1 và y=-x+3 trên và một mặt phẳng tọa độ.
b, hai tuyến đường thẳng y=x+1 và y=-x+3 cắt nhau trên C và cắt trục Ox theo đồ vật tự trên A cùng B. Search tọa độ của các điểm A, B, C.
c, Tính chu vi và mặc tích tam giác ABC.
Hướng dẫn giải
a, Đồ thị hàm số y=x+1 đi qua A(-1; 0) cùng (0; 1)
Đồ thị hàm số y=-x+3 trải qua B(3; 0) và (0; 3)
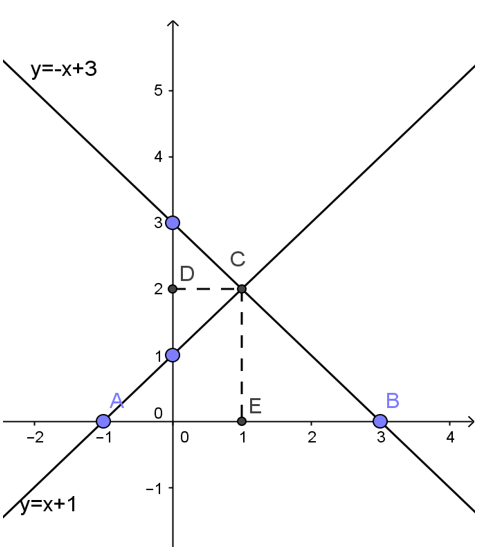
b, Với mặt đường thẳng y=x+1:
Cho y=0 ta suy ra x=-1. Vì chưng vậy, mặt đường thẳng cắt trục Ox trên A(-1; 0)
Với đường thẳng y=-x+3:
Cho y=0 ta tuy ra x=3. Vì vậy, mặt đường thẳng cắt trục Ox tại B(3; 0)
Gọi C (x; y) là giao điểm của con đường thẳng y=x+1 và con đường thẳng y=-x+3.
Vì C(x; y) nằm trong vào cả 2 đường trực tiếp trên buộc phải ta có: x+1=-x+3. Từ đó suy ra x=1
Thay x=1 vào hàm y=x+1 ta được y=2
Vậy C(1; 2)
Tham khảo thêm những Chuyên đề Toán lớp 9 khác:
ĐỀ THI, GIÁO ÁN, KHÓA HỌC DÀNH đến GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9
Bộ giáo án, bài giảng powerpoint, đề thi dành cho giáo viên cùng khóa học giành cho phụ huynh trên https://tailieugiaovien.com.vn/ . Cung cấp zalo Viet
Jack Official
Đồ thị của hàm số y = ax + b ( a ≠ 0 ) là 1 trong những đường thẳng cắt trục tung tại điểm bao gồm tung độ bởi b, tuy vậy song với đường thẳng y = ax giả dụ b ≠ 0 với trùng với mặt đường thẳng y = ax giả dụ b = 0.
Chú ý : Đồ thị hàm số bậc nhật y = ax + b (a ≠ 0 )còn được hotline là con đường thẳng y = ax + b ; b được call là tung độ nơi bắt đầu của đường thẳng.
2 . Phương pháp vẽ đồ dùng thị hàm số bậc nhất: y = ax + b (a ≠ 0 )
- lúc b = 0 thì y = ax. Đồ thị y = ax là con đường thẳng đi qua gốc tọa độ O(0;0) với điểm A(1;a) ( vẫn biết ).
- Xét trường đúng theo y = ax + b cùng với a ≠ 0 với b≠ 0.
Ta sẽ biết trang bị thị hàm số y = ax + b là 1 đường trực tiếp , cho nên vì vậy về hiệ tượng ta chỉ việc xác định được nhị điểm sáng tỏ nào kia của đồ dùng thị rồi vẽ đường thẳng qua hai điểm đó.
+ Cách trước tiên :
Xác định hai điểm bất kể của trang bị thị, ví dụ điển hình :
Cho x = 1, tính được y = a + b, ta tất cả điểm A(1 ; a + b)
Cho x = -1 , tính được y = -a + b, ta bao gồm điểm B(-1 ; b – a)
+ cách thứ nhì :
Xác định giao điểm của trang bị thị với nhị trục tọa độ :
Cho x = 0, tính được y = b, ta có điểm C(0;b)
Cho y = 0, tính được x = <-fracba>, ta tất cả điểm (<-fracba>;0)
Vẽ mặt đường thẳng qua A; B hoặc qua C; D ta được vật thị của hàm số y = ax + b
Dạng đồ thị của hàm số y = ax + b (a ≠ 0 )

II . Bài xích tập ví dụ như :
ví dụ 1 : cho các hàm số sau : y = 2x -3 với y = -3x + 4.
a, Vẽ đồ gia dụng thị những hàm số trên.
b, Điểm nào dưới đây thuộc đồ thị hàm số trên?
Giải
a,

b, thay
Vậy điểm A thuộc thiết bị thị hàm số y = 2x – 3.
- Điểm B thuộc thiết bị thị hàm số y = 2x – 3.
lấy ví dụ như 2 : a, Vẽ đồ thị các hàm số sau trên cùng mặt phẳng tọa độ:
b, gọi giao điểm của con đường thẳng
Giải

b, < an widehatOCB=2Rightarrow widehatOCBapprox 63^circ >
< an widehatOAB=frac43Rightarrow widehatOABapprox 53^circ >
lấy ví dụ 3: mang lại hàm số
a, Vẽ vật thị (D) của hàm số f(x).
b, Điểm nào sau đây nằm bên trên (D):
c, tìm tọa độ điểm M ϵ (D) cùng N ϵ (D) khi biết :
Giải

b, Điểm B và C vị trí (D).
c, cố gắng
Vậy
III . Bài bác tập từ bỏ luyện :
bài bác 1: a, Vẽ thứ thị những hàm số : y = x – 3; y = 3x – 3; y = -2x -3 Trên và một mặt phẳng tọa độ.
b, bao gồm nhận xét gì về vật dụng thị các hàm số này ?
bài xích 2 : mang lại hàm số y = (3-2m)x – 1.
a, với cái giá trị như thế nào của m thì hàm số đồng biến?
b, với cái giá trị nào của m thì hàm số nghịch vươn lên là ?
c, khẳng định giá trị của m chứa đồ thị hàm số trải qua điểm A(-2;-3).
d, Vẽ thứ thị hàm số với giá trị m vừa kiếm được ở (c).
bài bác 3: a, Vẽ trên thuộc hệ trục tọa độ Oxy đồ gia dụng thị những hàm số sau : y = 2x + 4 ; y = -x + 1 .b, tìm kiếm tọa độ giao điểm của hai đường thẳng trên.
bài xích 4 : a, Vẽ vật dụng thị hàm số y = x – 2 (d).
b, Tính khoangr cách từ gốc tọa độ đến đường thẳng (d).
bài 5 : a, Vẽ trên cùng hệ trục tọa độ Oxy đồ thị hàm số sau : y = x + 4 ; y= -x + 2 .
b, kiếm tìm tọa độ giao điểm M của hai tuyến đường thẳng;
c, gọi giao điểm của mặt đường thẳng y = x + 4 cùng với trục Ox, Oy the lắp thêm tự là A, B . Gọi giao điểm của con đường thẳng y = -x +2 với Õ là C . TÍnh diện tích tam giác ABC.
bài 6 : Vẽ tập hợp những điểm M(x;y) có tọa độ vừa lòng phương trình :
bài bác 7 : a, Vẽ trang bị thị của hàm số y = | x – 1 | + | x – 3 |.
Xem thêm: Tổng Hợp 101+ Hình Nền Cặp Đôi Tình Yêu, Cute Dễ Thương, 10000+ Tình Yêu Lãng Mạn & Ảnh Trái Tim Miễn Phí
b, Định quý hiếm của m nhằm phương trình :
| x – 1 | + | x – 3 | = 0 gồm đúng một nghiệm dương.
bài viết gợi ý:1. Hàm số bậc nhất 2. Các bài toán nâng cấp chuyên đề hệ thức Viet 3. Căn bậc tía 4. Tương tác giữa phép phân tách và khai phương 5. Rút gọn gàng biểu thức căn bậc hai 6. Thay đổi đơn giản căn thức bậc nhì 7. Contact giữa phép nhân và phép khai phương