Kết luận: Khi cùng tổng hai số với số trang bị ba, ta có thể cộng số thứ nhất với tổng nhị số còn lại.
Bạn đang xem: Công thức toán học lớp 5
Công thức tổng quát: (a + b) + c = a + (b + c)
3. Tính chất: cộng với 0:
Kết luận: Bất kì một số trong những cộng cùng với 0 cũng bằng chính nó.
CTTQ: a + 0 = 0 + a = a
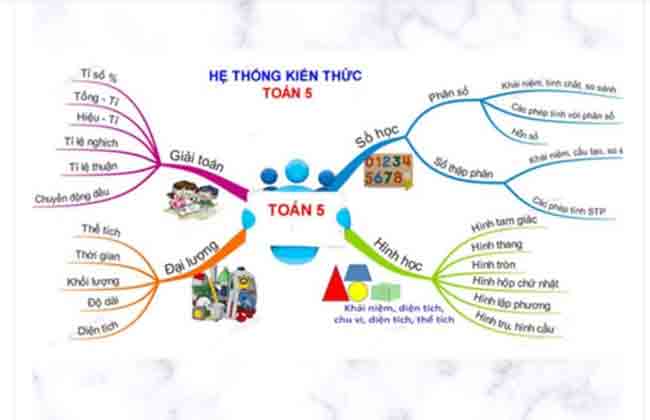
B. Phép trừ
I. Cách làm tổng quát:
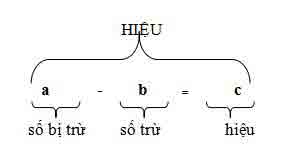
II. Tính chất:
1. Trừ đi 0:
Kết luận: Bất kì một trong những trừ đi 0 vẫn bởi chính nó.
CTTQ: a – 0 = a
2. Trừ đi thiết yếu nó:
Kết luận: một trong những trừ đi chủ yếu nó thì bởi 0.
CTTQ: a – a = 0
3. Trừ đi một tổng:
Kết luận: lúc trừ một trong những cho một tổng, ta có thể lấy số kia trừ dần từng số hạng của tổng đó.
CTTQ: a – (b + c) = a – b – c = a – c – b
4. Trừ đi một hiệu:
Kết luận: lúc trừ một số trong những cho một hiệu, ta hoàn toàn có thể lấy số kia trừ đi số bị trừ rồi cùng với số trừ.
CTTQ: a – (b – c) = a – b + c = a + c – b
C. Phép nhân
I. Phương pháp tổng quát
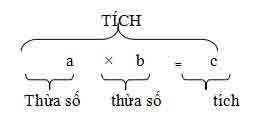
II. Tính chất:
1. đặc điểm giao hoán:
Kết luận: Khi đổi chỗ những thừa số vào một tích thì tích không gắng đổi.
CTTQ: a × b = b × a
2. đặc điểm kết hợp:
Kết luận: muốn nhân tích nhì số cùng với số trang bị ba, ta rất có thể nhân số đầu tiên với tích nhì số còn lại.
CTTQ: (a × b) × c = a × (b × c)
3. Tính chất: nhân với 0:
Kết luận: Bất kì một trong những nhân cùng với 0 cũng bởi 0.
CTTQ: a × 0 = 0 × a = 0
4. Tính chất nhân với 1:
Kết luận: một số trong những nhân với một thì bằng chính nó.
CTTQ: a × 1 = 1 × a = a
5. Nhân với 1 tổng:
Kết luận: lúc nhân một số trong những với một tổng, ta rất có thể lấy số kia nhân với từng số hạng của tổng rồi cùng các công dụng với nhau.
CTTQ: a × (b + c) = a × b + a × c
6. Nhân với một hiệu:
Kết luận: lúc nhân một số với một hiệu, ta rất có thể lấy số kia nhân với số bị trừ và số trừ rồi trừ hai kết quả cho nhau.
CTTQ: a × (b – c) = a × b – a × c
D. Phép chia
I. Bí quyết tổng quát:
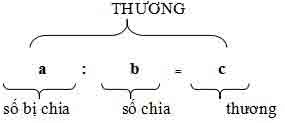
Phép chia còn dư:
a : b = c (dư r)
số bị chia số phân tách thương số dư
Chú ý: Số dư phải nhỏ hơn số chia.
II. Công thức:
1. Phân chia cho 1:Bất kì một số trong những chia cho một vẫn bởi chính nó.
CTTQ: a : 1 = a
2. Phân chia cho bao gồm nó:Một số phân tách cho bao gồm nó thì bởi 1.
CTTQ: a : a = 1
3. 0 phân chia cho một số:0 phân tách cho một số trong những bất kì khác 0 thì bằng 0
CTTQ: 0 : a = 0
4. Một tổng phân chia cho một số:Khi phân tách một tổng cho một số, giả dụ cácsố hạng của tổng hồ hết chia hết đến số đó, thì ta hoàn toàn có thể chia từng số hạng mang đến số phân chia rồi cộng các hiệu quả tìm được với nhau.
CTTQ: (b + c) : a = b : a + c : a
5. Một hiệu chia cho một số:Khi chia một hiệu cho 1 số, nếu như số bị trừ với số trừ đều chia hết mang đến số đó, thì ta rất có thể lấy số bị trừ với số trừ chia cho số kia rồi trừ hai kết quả cho nhau.
CTTQ: (b – c) : a = b : a – c : a
6. Chia một số trong những cho một tích:Khi chia một số trong những cho một tích, ta hoàn toàn có thể chia số đó cho 1 thừa số, rồi lấy công dụng tìm được phân tách tiếp mang lại thừa số kia.
CTTQ: a :(b × c) = a : b : c = a : c : b
7. Phân tách một tích cho 1 số:Khi chia một tích cho 1 số, ta hoàn toàn có thể lấy một vượt số phân chia cho số đó (nếu chia hết), rồi nhân công dụng với quá số kia.
CTTQ: (a × b) : c = a : c × b = b : c × a
E. đặc điểm chia hết
1, phân tách hết đến 2: các số gồm tận cùng là 0, 2, 4, 6, 8 (là các số chẵn) thì phân tách hết mang lại 2.
VD: 312; 54768;….
2, phân tách hết mang đến 3: những số bao gồm tổng các chữ số chia hết mang đến 3 thì phân tách hết mang đến 3.
VD: đến số 4572
Ta có 4+ 5 + 7+ 2 = 18; 18 : 3 = 6 cần 4572 : 3 = 1524
3, chia hết mang lại 4: những số tất cả hai chữ số tận cùng phân chia hết mang đến 4 thì phân chia hết mang lại 4.
VD: mang lại số: 4572
Ta gồm 72 : 4 = 18 buộc phải 4572 : 4 = 11 4 3
4, phân tách hết mang đến 5: các số bao gồm tận cùng là 0 hoặc 5 thì chia hết mang đến 5.
VD: 5470; 7635
5, phân chia hết đến 6 (Nghĩa là phân tách hết đến 2 cùng 3): những số chẵn và gồm tổng các chữ số phân chia hết mang lại 3 thì phân tách hết mang lại 6.
VD: mang đến số 1356
Ta có 1+3+5+6 =15; 15:3 = 5 yêu cầu 1356 : 3 = 452
6, phân tách hết cho 10 (Nghĩa là phân chia hết mang đến 2 cùng 5): các số tròn chục (có hàng đơn vị bằng 0) thì phân chia hết mang đến 10.
VD: 130; 2790
7, chia hết đến 11: Xét tổng những chữ số ở hàng chẵn bằng tổng các chữ số ở sản phẩm lẻ thì số đó chia hết mang lại 11.
VD: mang đến số 48279
Ta có 4 + 2 + 9 = 8 + 7 = 15 đề xuất 48279 : 11 = 4389
8, phân tách hết mang đến 15 (Nghĩa là phân tách hết đến 3 với 5): những số bao gồm chữ số hàng đơn vị là 0 (hoặc 5) với tổng các chữ số phân chia hết mang đến 3 thì phân tách hết mang lại 15.
VD: cho số 5820
Ta có 5 + 8 + 2 + 0 = 15; 15 : 3 = 5 phải 5820 : 15 = 388
9, phân chia hết mang lại 36 (Nghĩa là chia hết mang đến 4 và 9): các số có hai chữ số tận cùng phân tách hết mang đến 4 với tổng những chữ số phân tách hết đến 9 thì chia hết mang đến 36.
VD: cho số: 45720
Ta có đôi mươi : 4 = 5 cùng (4 + 5 + 7 + 2 + 0) = 18
18 : 9 = 2 cần 45720 : 36 = 1270
F. Toán trung bình cộng
1. Mong mỏi tìm trung bình cùng (TBC) của khá nhiều số, ta tính tổng của những số đó rồi phân tách tổng đó cho số những số hạng.
CTTQ: TBC = tổng những số : số những số hạng
2. Kiếm tìm tổng các số: ta rước TBC nhân số các số hạng
CTTQ: Tổng những số = TBC × số các số hạng
Tìm nhì số lúc biết tổng cùng hiệu của nhị số đó
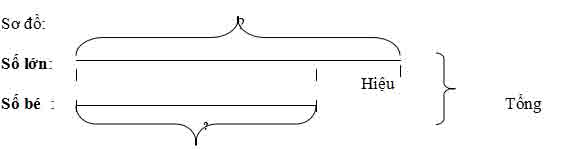
Cách 1:
Tìm số lớn = (Tổng + hiệu) : 2
Tìm số bé = số to – hiệu
hoặc số nhỏ nhắn = tổng – số lớn
Cách 2:
Tìm số bé nhỏ = (tổng – hiệu) : 2
Tìm số to = số bé nhỏ + hiệu
hoặc số bự = tổng – số bé
Tìm nhì số khi biết tổng và tỉ số của hai số đó
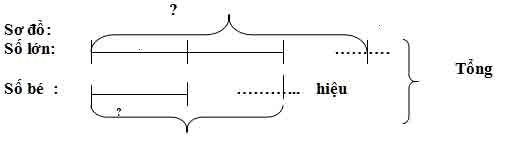
Cách làm:
Bước 1: tìm kiếm tổng số phần đều nhau = lấy số phần số to + số phần số bé
Bước 2: tra cứu số bé bỏng = lấy tổng : toàn bô phần bằng nhau × số phần số bé
Bước 3: kiếm tìm số bự = rước tổng – số bé
Tìm hai số khi biết hiệu và tỉ số của nhị số đó
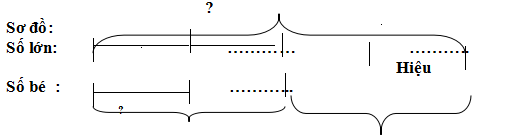
Cách làm:
Bước 1: kiếm tìm hiệu số phần đều bằng nhau = rước số phần số phệ – số phần số bé
Bước 2: kiếm tìm số nhỏ nhắn = mang hiệu : hiệu số phần bằng nhau × số phần số bé
Bước: tìm kiếm số béo = đem hiệu + số bé
G. Toán tỉ lệ thuận
1. Khái niệm: nhì đại lượng tỉ lệ thành phần thuận lúc đại lượng này tăng (hoặc giảm) từng nào lần thì đại lượng kia cũng tăng (hoặc giảm) đi từng ấy lần.
2. Việc mẫu: Một ô tô trong hai giờ đi được 90km. Hỏi trong 4 giờ ô tô đó đi được bao nhiêu ki- lô- mét?
Tóm tắt:
2 giờ: 90 km
4 giờ: … km?
Bài giải
Cách 1:
Trong một giờ xe hơi đi được là:
90 : 2 = 45 (km) (*)
Trong 4 giờ ô tô đi được là:
45 × 4 = 180 (km)
Đáp số: 180 km
Cách 2:
4 giờ gấp 2 tiếng số lần là:
4 : 2 = 2 (lần) (**)
Trong 4 giờ ô tô đi được là:
90 × 2 = 180 (km)
Đáp số: 180 km
(*) đoạn này là cách “ rút về solo vị” (**) đoạn này là cách “ search tỉ số”
H. Toán tỉ lệ thành phần nghịch
1. Khái niệm: hai đại lượng tỉ lệ nghịch lúc đại lượng này tăng (hoặc giảm) bao nhiêu lần thì đại lượng cơ lại sút (hoặc tăng) từng ấy lần.
2. Câu hỏi mẫu: ước ao đắp xong nền đơn vị trong hai ngày, cần phải có 12 người. Hỏi hy vọng đắp xong nền nhà đó trong 4 ngày thì cần phải có bao nhiêu người? (Mức làm cho của mỗi người như nhau)
Tóm tắt:
2 ngày: 12 người
4 ngày: …. Người?
Bài giải
Cách 1:
Muốn đắp dứt nền nhà trong 1 ngày, đề nghị số fan là:
12 × 2 = 24 (người) (*)
Muốn đắp ngừng nền nhà trong 4 ngày, yêu cầu số người là:
24 : 4 = 6 (người)
Đáp số: 6 người
(*) bước này là bước “ rút về 1-1 vị”
Cách 2:
4 ngày vội 2 ngày mốc giới hạn là:
4 : 2 = 2 (lần) (**)
Muốn đắp kết thúc nền nhà trong 4 ngày, đề xuất số fan là:
12 : 2 = 6 (người)
Đáp số: 6 người
(**) đoạn này là bước “ tra cứu tỉ số”
I. Kiếm tìm phân số của một số
KL: ý muốn tìm phân số của một số, ta rước số đó nhân cùng với phân số đang cho.
Công thức tổng quát: giá trị a/b của A = A × a/b
VD: vào rổ gồm 12 quả cam. Hỏi 2/3 số cam vào rổ là bao nhiêu?
Giải
2/3 Số cam trong rổ là:
12 × 2/3 = 8 (quả)
ĐS: 8 quả
K. Tìm một số trong những biết cực hiếm phân số của số đó
KL: muốn tìm một vài khi biết một quý giá phân số của số đó, ta lấy giá trị đó phân chia cho phân số.
CTTQ:
Giá trị a/b của A = giá trị của phân số : a/b
VD: cho 2/3 số cam trong rổ cam là 8 quả. Hỏi rổ cam đó gồm bao nhiêu quả?
Giải
Số cam vào rổ là:
8 : 2/3 = 12 (quả)
ĐS: 12 quả
L. Tỉ số phần trăm
1. Kiếm tìm tỉ số xác suất của nhì số: ta có tác dụng như sau:
– tìm kiếm thương của nhị số kia dưới dạng số thập phân.
– Nhân thương kia với 100 và viết thêm kí hiệu tỷ lệ (%) vào bên đề nghị tích kiếm tìm được.
CTTQ: a : b = T (STP) = STP × 100 (%)
VD: search tỉ số phần trăm của 315 cùng 600
Giải
Tỉ số tỷ lệ của 315 cùng 600 là:
315 : 600 = 0,525 = 52,5 %
ĐS: 52,5 %
2. Tìm giá trị xác suất của một trong những cho trước:ta đem số đó phân tách cho 100 rồi nhân cùng với số phần trăm hoặc mang số đó nhân với số phần trăm rồi chia cho 100.
CTTQ: giá trị % = Số A : 100 × số % hoặc quý giá % = Số A × số % : 100
VD: trường Đại Từ tất cả 600 học tập sinh. Số học sinh nữ chiếm 45% số học viên toàn trường. Tính số học sinh nữ của trường.
Giải
Số học sinh của trường đó là:
600 : 100 × 45 = 270 (học sinh)
ĐS: 270 học tập sinh
3. Tìm một số trong những biết giá bán trị phần trăm của số đó:ta rước giá trị tỷ lệ của số đó phân chia cho số tỷ lệ rồi nhân cùng với 100 hoặc ta mang giá trị tỷ lệ của số đó nhân với 100 rồi phân tách cho số phần trăm.
CTTQ: Số A = quý hiếm % : số phần trăm × 100 hoặc Số A = cực hiếm % × 100 : số phần trăm
VD: Tìm một số trong những biết 30% của nó bởi 72.
Giải
Giá trị của số đó là:
72 : 30 × 100 = 240
ĐS: 240
M. Bảng đơn vị đo độ dài
1. Bảng đơn vị đo độ dài:
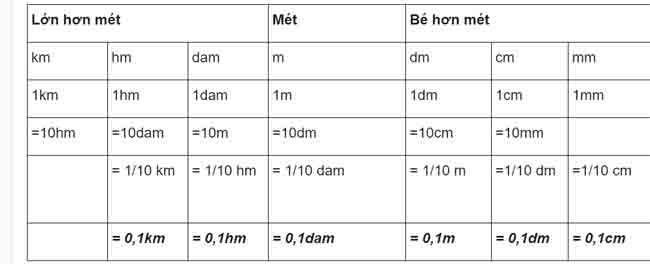
2.Nhậnxét:
Hai đơn vị đo độ nhiều năm liền nhau gấp (hoặc kém) nhau 10 lần.VD: 1m = 10 dm
1cm = 1/10 dm = 0,1 dm
Mỗi đơn vị đo độ nhiều năm ứng với một chữ số.VD: 1245m = 1km 2hm 4dam 5m
N. Bảng đơn vị đo khối lượng
1. Bảng đơn vị đo khối lượng:
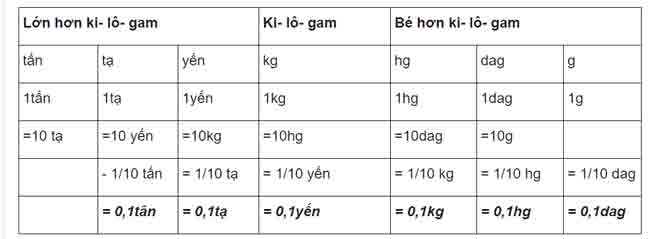
2. Nhậnxét:
Hai đơn vị chức năng đo khối lượng liền nhau vội vàng (hoặc kém) nhau 10 lần.VD: 1kg = 10 hg
1g = 1/10 dag = 0,1dag
Mỗi đơn vị chức năng đo trọng lượng ứng với 1 chữ số.VD: 1245g = 1kg 2hg 4dag 5g
O. Bảng đơn vị đo diện tích
1. Bảng đơn vị đo diện tích:
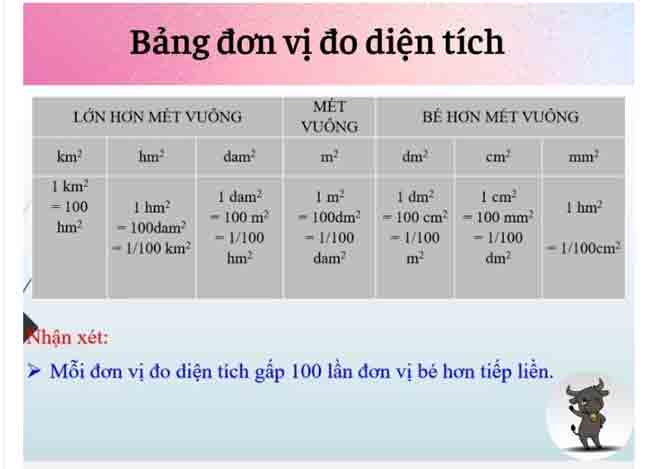
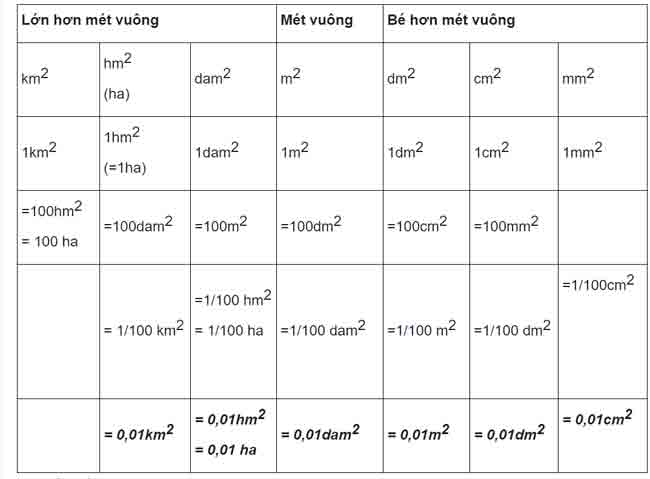
2. Nhậnxét:
Hai đơn vị đo diện tích liền nhau gấp (hoặc kém) nhau 100 lần.VD: 1m2= 100 dm2
1cm2= 1/100 dm2= 0,01dm2
Mỗi đơn vị chức năng đo độ dài ứng với nhị chữ số.VD: 1245m2= 12dam245m2
P. Bảng đơn vị chức năng đo thể tích
| Mét khối | Đề –xi -mét khối | xăng- ti- mét khối |
| 1m3 | 1dm3 | 1cm3 |
| = 1000 dm3 | = 1000 cm3 | |
| = 1/1000 m3 | = 1/1000 dm3 | |
| = 0,001m3 | = 0,001dm3 |
Nhậnxét:
Hai đơn vị đo thể tích ngay thức thì nhau vội (hoặc kém) nhau 1000 lần.VD: 1m3= 1000 dm3
1cm3= 1/1000 dm3= 0,001dm3
Mỗi đơn vị chức năng đo diện tích ứng với bố chữ số.VD: 1245dm3= 1m3245dm3Lưu ý: 1dm3= 1l
R. HÌNH VUÔNG
1. Tính chất:Hình vuông là tứ giác gồm 4 góc vuông, 4 cạnh dài bởi nhau.
Cạnh kí hiệu là a
2.Tính chu vi:Muốn tính chu vi hình vuông, ta đem số đo một cạnh nhân với 4.
CTTQ: phường = a × 4
Muốn tra cứu một cạnh hình vuông, ta mang chu vi phân chia cho 4. A = phường : 4
3. Tính diện tích: ý muốn tính diện tích hình vuông , ta mang số đo một cạnh nhân với bao gồm nó.
CTTQ: S = a × a
· mong tìm 1 cạnh hình vuông, ta kiếm tìm xem một số trong những nào kia nhân với bao gồm nó bằng diện tích, thì chính là cạnh.
· VD: mang đến diện tích hình vuông là 25 m2. Tìm cạnh của hình vuông vắn đó.
Giải
Ta tất cả 25 = 5 × 5; vậy cạnh hình vuông vắn là 5m
S. HÌNH CHỮ NHẬT
1. Tính chất:Hình chữ nhật là tứ giác bao gồm 4 góc vuông, 2d dài bởi nhau, 2 chiều rộng bằng nhau.
Kí hiệu chiều dài là a, chiều rộng lớn là b
2. Tính chu vi: hy vọng tính chu vi hình chữ nhật, ta rước số đo chiều dài cộng số đo chiều rộng
(cùng đơn vị chức năng đo) rồi nhân với 2.
CTTQ: p = (a + b) × 2
* ý muốn tìm chiều dài, ta đem chu vi chia cho 2 rồi trừ đi chiều rộng a = phường : 2 – b
· ước ao tìm chiều rộng, ta mang chu vi chia cho 2 rồi trừ đi chiều dài.
b = p. : 2 – a
3. Tính diện tích: mong mỏi tính diện tích hình chữ nhật , ta rước số đo chiều lâu năm nhân với số đo chiều rộng lớn (cùng đơn vị chức năng đo).
CTTQ: S = a × b
· mong mỏi tìm chiều dài, ta lấy diện tích chia đến chiều rộng. A = S : b
· mong tìm chiều rộng, ta lấy diện tích s chia cho chiều dài.
b = S : a
T. Hình bình hành
Tính chất: Hình bình hành tất cả hai cặp
cạnh đối diện tuy vậy song và bởi nhau.
Kí hiệu: Đáy làa,
chiều cao làh
Tính chu vi: Chu vi hình bình hành là tổng độ nhiều năm của 4 cạnh
Tính diện tích: muốn tính diện tích s hình bình hành, ta rước độ dài đáy nhân với chiều cao (cùng đơn vị chức năng đo)
CTTQ: S = a×h
– Muốntìm độ dài đáy, ta lấy diện tích chia mang lại chiều cao.
a = S : b
– Muốntìm chiều rộng, ta lấy diện tích chia mang lại chiều dài.
b = S : a
U. Hình thoi
Tính chất:
Hình thoi có hai cặp cạnh đối diện tuy vậy song và tư cạnh bằng nhau
Hình thoi bao gồm hai đường chéo vuông góc cùng nhau và cắt nhau trên trung điểm của mỗi đường.
Kí hiệu hai đường chéo cánh làmvàn
Tính chu vi: hy vọng tính chu vi hình thoi, ta mang số đo một cạnh nhân với 4.
Tính diện tích: diện tích hình thoi bằng tích của độ nhiều năm hai đường chéo chia đến 2 (cùng đơn vị đo).
V. Hình thang
Tính chất: Hình thang gồm một cặp cạnh đối diện tuy nhiên song.
– Chiều cao: là đoạn thẳng trọng tâm hai đáy cùng vuông góc với hai đáy.
Kí hiệu: đáy phệ làa, đáy bé dại làb,chiều cao làh
Tính diện tích: ước ao tính diện tích hình thang ta lấy tổng độ dài hai lòng nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.
S = (a + b)×h : 2
Hoặc:Muốn tính diện tích s hình thang ta đem trung bình cộng hai lòng nhân cùng với chiều cao.
S =×h
– Tính tổng nhị đáy:Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.
(a + b) = S×2 : h
– Tính trung bình cùng hai đáy:Ta lấy diện tích chia mang đến chiều cao.
= S : h
– Tính độ dài đáy lớn:Ta lấy diện tích nhân cùng với 2, phân chia cho độ cao rồi trừ đi độ lâu năm đáy bé.
a = S×2 : h – b
– Tính độ dài đáy bé:Ta lấy diện tích s nhân với 2, chia cho độ cao rồi trừ đi độ lâu năm đáy lớn.
b = S×2 : h – a
– Tính chiều cao:Ta lấy diện tích nhân cùng với 2 rồi phân tách cho tổng độ lâu năm hai đáy.
h = S×2 : (a + b)
hoặc: Tính chiều cao:Ta lấy diện tích s chia cho trung bình cùng của hai đáy.
X. Hình tam giác
Tính chất: Hình tam giác có bố cạnh, 3 góc, 3 đỉnh.
Chiều cao là đoạn thẳng hạ từ bỏ đỉnh vuông góc với cạnh đối diện.
Kí hiệu lòng làa, chiều cao làh
Tính chu vi: Chu vi hình tam giác là tổng độ lâu năm của 3 cạnh.
Tính diện tích: ý muốn tính diện tích hình tam giác ta rước độ nhiều năm đáy nhân với độ cao (cùng đơn vị chức năng đo) rồi chia cho 2.
S = a×h : 2
– Tính cạnh đáy:Ta lấy diện tích nhân với 2 rồi phân tách cho chiều cao.
a = S×2 : h
– Tính chiều cao:Ta lấy diện tích s nhân cùng với 2 rồi phân tách cho cạnh đáy.
h = S×2 : a
Y. Hình tròn
1. Tính chất: hình tròn có tất cả các bán kính bằng nhau.
– Đường bao bọc hình tròn hotline là đường tròn.
– Điểm ở vị trí chính giữa hình tròn là tâm.
– Đoạn thẳng nối trọng tâm với một điểm trê tuyến phố tròn điện thoại tư vấn là buôn bán kính. Ki hiệu làr
– Đoạn thẳng trải qua tâm với nối hai điểm của con đường tròn call là đường kính.
Đường kính gấp rất nhiều lần lần chào bán kính. Kí hiệu làd
2. Tính chu vi: ước ao tính chu vi hình tròn trụ ta lấy đường kính nhân với số 3,14.
C = d×3,14
Hoặc ta lấy nửa đường kính nhân 2 rồi nhân cùng với số 3,14.
C = r×2×3,14
Tính đường kính: ta lấy chu vi phân tách cho số 3,14
d = C : 3,14
Tính bán kính: ta rước chu vi phân tách cho 2 rồi phân tách cho số 3,14
r = C : 2 : 3,14(Tính ra nháp: r = C : 6,28)
3. Tính diện tích: mong muốn tính diện tích hình trụ ta lấy nửa đường kính nhân với nửa đường kính rồi nhân cùng với số 3,14.S = r×r×3,14
–Biết diện tích, muốntìm chào bán kính, ta làm như sau: Lấy diện tích s chia đến số 3,14 nhằm tìm tích của hai nửa đường kính rồi tìm kiếm xem số nào đó nhân với chủ yếu nó bởi tích đó thì đấy là bán kính hình tròn.
VD: Cho diện tích s một hình tròn bằng 28,26 cm2. Tìm buôn bán kính hình tròn đó.
Giải
Tích hai chào bán kính hình trụ là:
28,26 : 3,14 = 9 (cm2)
Vì 9 = 3 × 3 nên chào bán kính hình tròn là 3cm
Hình hộp chữ nhật
1. Tính chất: Hình hộp chữ nhật bao gồm 6 mặt, hai dưới mặt đáy và bốn mặt bên.
– gồm 8 đỉnh, 12 cạnh
– Có cha kích thước: chiều dài (a), chiều rộng lớn (b), chiều cao (c).
2. Tính diện tíchxung quanh: ao ước tính diện tích xung xung quanh hình hộp chữ nhật ta mang chu vi đáy nhân với chiều cao (cùng một đơn vị đo).
S×q = P(đáy)×c
Hoặc: S×q = (a + b)×2×c
– mong tìmchu vi đáy, ta lấy diện tích s xung quanh phân chia cho chiều cao.
P(đáy) = S×q : c
– mong tìmchiều cao, ta lấy diện tích s xung quanh chia cho chu vi đáy
c = S×q : p. (đáy)
– ước ao tìmtổng hai đáy, ta lấy diện tích s xung quanh chia cho 2 rồi chia cho chiều cao.
(a + b) = S×q : 2 : h
– mong mỏi tìmchiều dài, ta lấy diện tích xung quanh phân tách cho 2, phân chia cho độ cao rồi trừ đi chiều rộng.
a = S×q : 2 : c – b
– mong muốn tìmchiều rộng, ta lấy diện tích s xung quanh phân chia cho 2, chia cho chiều cao rồi trừ đi chiều dài.
b = S×q : 2 : c – a
– Tính diện tích toàn phần:Muốn tính diện tích s toàn phần hình vỏ hộp chữ nhật ta lấy diện tích xung quanh cộng diện tích hai đáy.
Stp = S×q + S(2đáy)
Hoặc:Stp = (a + b )×2×c + a×b×2
–Muốn tìmdiện tích đáyta mang chiều dài nhân với chiều rộng.
S(đáy) = a×b
– mong mỏi tìmchiều dài,ta lấy diện tích s đáy phân tách cho chiều rộng.
a = S(đáy) : b
– mong muốn tìmchiều rộng,ta lấy diện tích s đáy phân tách cho chiều dài.
b = S(đáy) : a
4. Tính thể tích hình hộp chữ nhật:ta đem chiều lâu năm nhân cùng với chiều rộng lớn rồi nhân với độ cao (cùng một đơn vị chức năng đo).
V = a×b×c
– mong tìmchiều dài,ta rước thể tích phân tách cho chiều rộng lớn rồi phân chia tiếp mang đến chiều cao.
a = V : b : c
– mong muốn tìmchiều rộng,ta rước thể tích phân tách cho chiều lâu năm rồi chia tiếp mang đến chiều cao.
b = V : a : c
– ước ao tìmchiều cao,ta đem thể tích phân tách cho chiều nhiều năm rồi chia tiếp mang lại chiều rộng.
c = V : a : b
hoặc đem thể tích phân tách cho diện tích s đáy
c = V : S(đáy)
Hình lập phương
1. Tính chất: Hình lập phương có 6 mặt là các hình vuông vắn bằng nhau.
– bao gồm 8 đỉnh, 12 cạnh dài bằng nhau. Kí hiệu cạnh làa
2. Tính diện tích×ung quanh: ước ao tính diện tích s ×ung xung quanh hình lập phương ta lấy
diện tích một khía cạnh nhân cùng với 4:S×q = S(1 mặt)×4
3. Tính diện tích toàn phần: ao ước tính diện tích s toàn phần hình lập phương ta lấy diện tích s một mặt nhân cùng với 6:Stp = S(1 mặt)×6
Muốn tìmdiện tích một mặtta lấy diện tích ×ung quanh chia cho 4 hoặc diện tích toàn phần chia cho 6.
S(1 mặt) = S×q : 4
Hoặc: S(1 mặt) = Stp : 6
– Muốntìm 1 cạnh hình lập phương, ta kiếm tìm xem một số nào đó nhân với bao gồm nó bằng diện tích một mặt, thì đó là cạnh.
–VD: Cho diện tích một khía cạnh là 25 m2. Tìm cạnh của hình lập phương đó.
Giải
Ta bao gồm 25 = 5 × 5;
vậy cạnh hình lập phương là 5m
4.Tính thể tích hình lập phương:ta lấy cạnh nhân cùng với cạnh rồi nhân cùng với cạnh.
V = a×a×a
Muốntìm 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó rồi nhân tiếp với nó bằng thể tích, thì chính là cạnh.
Lớp 1Tài liệu Giáo viên
Lớp 2Lớp 2 - liên kết tri thức
Lớp 2 - Chân trời sáng tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - liên kết tri thức
Lớp 3 - Chân trời sáng tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Tài liệu Giáo viên
Lớp 4Lớp 4 - kết nối tri thức
Lớp 4 - Chân trời sáng tạo
Lớp 4 - Cánh diều
Tiếng Anh lớp 4
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - liên kết tri thức
Lớp 6 - Chân trời sáng sủa tạo
Lớp 6 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 7Lớp 7 - liên kết tri thức
Lớp 7 - Chân trời sáng sủa tạo
Lớp 7 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 8Lớp 8 - liên kết tri thức
Lớp 8 - Chân trời sáng sủa tạo
Lớp 8 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - kết nối tri thức
Lớp 10 - Chân trời sáng sủa tạo
Lớp 10 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 11Lớp 11 - kết nối tri thức
Lớp 11 - Chân trời sáng tạo
Lớp 11 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
gia sưLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Công thức, Định nghĩa Toán, Lí, Hóa
Đường thẳng
Hình tam giác
Các trường hòa hợp tam giác bởi nhau
Hình thang
Hình bình hành
Hình thoi
Hình chữ nhật
Tổng hợp kiến thức cơ phiên bản Toán lớp 5 học tập kì 1, học kì 2 bỏ ra tiết
ÔN TẬP VÀ BỔ SUNG VỀ PHÂN SÔ
1. Các đặc điểm cơ bạn dạng của phân số
*) ví như nhân cả tử số và mẫu mã số của một phân số với cùng một số trong những tự nhiên khác thì được một phân số bằng phân số đang cho.
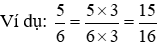
*) Nếu phân chia cả tử số và mẫu số của một phân số cùng với cùng một trong những tự nhiên không giống thì được một phân số bởi phân số đã cho.
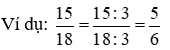
2. Rút gọn phân số
Phương pháp:
+ Xét coi tử số và mẫu mã số cùng chia hết mang lại số tự nhiên và thoải mái nào to hơn 1.
+ phân tách tử số và chủng loại số mang đến số đó.
+ Cứ có tác dụng như thế cho tới khi nhận ra phân số buổi tối giản.
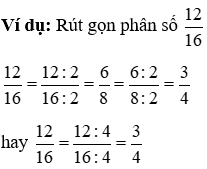
3. Quy đồng mẫu mã số của các phân số
Phương pháp:
+ Lấy tử số và mẫu mã số của phân số thứ nhất nhân với chủng loại số của phân số lắp thêm hai.
+ Lấy tử số và mẫu số của phân số sản phẩm công nghệ hai nhân với mẫu mã số của phân số sản phẩm nhất.

4. đối chiếu hai phân số
4.1. So sánh hai phân số cùng mẫu số
Trong nhị phân số cùng mẫu mã số:
· Phân số nào có tử số nhỏ hơn thì nhỏ nhắn hơn.
· Phân số nào gồm tử số lớn hơn nữa thì lớn hơn.
· ví như tử số bằng nhau thì nhì phân số đó bởi nhau.
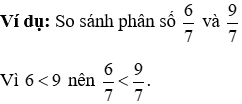
4.2. So sánh hai phân số không cùng chủng loại số
Muốn đối chiếu hai phân số khác mẫu số, ta hoàn toàn có thể quy đồng mẫu số nhị phân số đó, rồi so sánh các tử số của hai phân số mới.
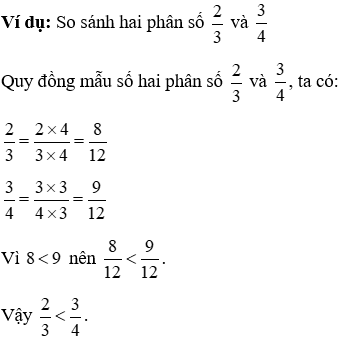
5. Phân số thập phân
Khái niệm: những phân số tất cả mẫu số là được gọi là phân số thập phân
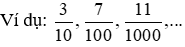
6. Phép cộng và trừ nhì phân số bao gồm cùng mẫu mã số
Phương pháp: hy vọng cộng (hoặc trừ) hai phân số cùng chủng loại số ta cùng (hoặc trừ) hai tử số với nhau và giữ nguyên mẫu số.

7. Phép cùng và trừ nhị phân số ko cùng chủng loại số
Phương pháp: mong muốn cộng (hoặc trừ) hai phân số khác mẫu mã số ta quy đồng chủng loại số, rồi cùng (hoặc trừ) hai phân số đã quy đồng mẫu số.

8. Phép nhân cùng phép chia hai phân số
● hy vọng nhân nhị phân số ta lấy tử số nhân với tử số, chủng loại số nhân với mẫu số.
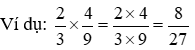
● mong mỏi chia nhị phân số cho một phân số ta rước phân số trước tiên nhân với phân số thứ hai hòn đảo ngược.
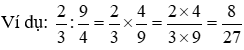
HỖN SỐ
1. Có mang hỗn số
Hỗn số có hai yếu tố là phân nguyên cùng phần phân số.
Ví dụ: lếu láo số
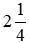
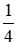
Chú ý: Phần phân số của hỗn số lúc nào cũng nhỏ tuổi hơn
2. Biện pháp chuyển hỗn số thành phân số
Phương pháp:
+ Tử số bởi phần nguyên nhân với mẫu số rồi cùng với tử số ở phần phân số.
+ chủng loại số bằng mẫu số tại vị trí phân số.

3. Cách chuyển phân số thành lếu số
Phương pháp:
+ Tính phép chia tử số mang lại mẫu số
+ giữ nguyên mẫu số của phần phân số; Tử số thông qua số dư của phép phân chia tử số mang lại mẫu số
+ Phần nguyên bởi thương của phép phân chia tử số mang lại mẫu số

4. Các phép toán với láo lếu số
4.1. Phép cộng, trừ hỗn số
Cách 1. đưa hỗn số về phân số
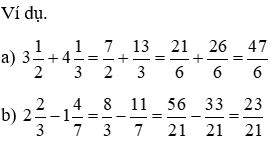
Cách 2. Bóc hỗn số nguyên tố nguyên và phần phân số
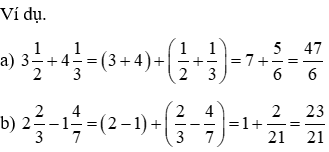
4.2. Phép nhân, phân tách hỗn số
Phương pháp: mong nhân (hoặc chia) nhì hỗn số, ta đưa hai láo số về dạng phân số rồi nhân (hoặc chia) nhị phân số vừa gửi đổi.
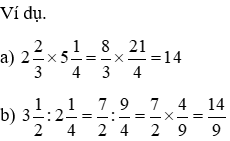
5. So sánh hỗn số
Cách 1. Gửi hỗn số về phân số
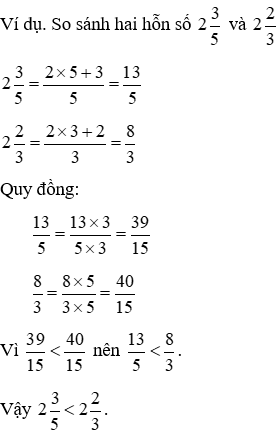
Cách 2. So sánh phần nguyên và phần phân số

SỐ THẬP PHÂN VÀ CÁC PHÉP TÍNH VỚI SỐ THẬP PHÂN
1. Khái niệm số thập phân
Ôn lại phân số thập phân: các phân số tất cả mẫu số là ,… được hotline là phân số thập phân.
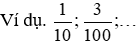
Mỗi số thập phân tất cả hai phần: Phần nguyên cùng phần thập phân (chúng được phân làn bởi vệt phẩy)
Ví dụ. Số thập phân 4,35 tất cả hai phần: Phần nguyên (4) cùng phần thập phân (35)
2. Chuyển những phân số thành số thập phân
Phương pháp: trường hợp phân số đã đến chưa là phân số thập phân thì ta chuyển những phân số thành phân số thập phân rồi gửi thành số thập phân.
Ví dụ. Chuyển các phân số sau thành phân số thập phân:

3. Nhảy số thập tạo thành phân số
Phương pháp: Viết số thập phân dưới dạng phân số thập phân kế tiếp thực hiện công việc rút gọn phân số thập phân đó.
(1, 2, 3 chữ số phần thập phân khi chuyển sang phân số thập phân có mẫu số là 10, 100, 100,…)
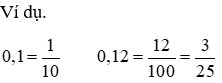
4. Viết những số đo độ dài, khối lượng… dưới dạng số thập phân
Phương pháp:
- kiếm tìm mối liên hệ giữa hai đơn vị đo vẫn cho.
- dịch số đo độ nhiều năm đã đến thành phân số thập phân có đơn vị chức năng đo lớn hơn.
- đưa từ số đo độ dài dưới dạng phân số thập chia thành số đo độ dài khớp ứng dưới dạng số thập phân có đơn vị chức năng lớn hơn.
Ví dụ. Viết số đo bên dưới dạng phân số thập phân và số thập phân
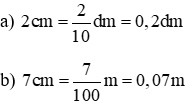
5. Viết hỗn số thành phân số thập phân
Phương pháp: Đổi lếu láo số về dạng phân số thập phân, sau đó chuyển thành số thập phân
Ví dụ. Viết hỗn số thành số thập phân:
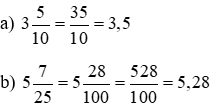
6. Phép cộng và phép trừ các số thập phân
6.1. Phép cùng hai số thập phân
Muốn cùng hai số thập phân ta làm như sau:
- Viết số hạng này dưới số hạng kia thế nào cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- cùng như cộng những số trường đoản cú nhiên.
- Viết vết phẩy làm việc tổng thẳng cột với các dấu phẩy của các số hạng.
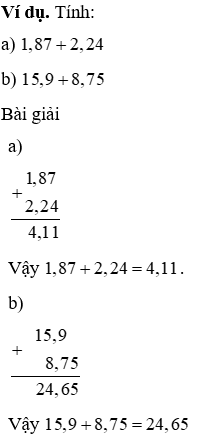
6.2. Phép trừ nhị số thập phân
Muốn trừ một vài thập phân cho một số trong những thập phân ta có tác dụng như sau:
- Viết số trừ bên dưới số bị trừ làm thế nào để cho các chữ số ở và một hàng để thẳng cột nhau.
- triển khai phép trừ như trừ những số trường đoản cú nhiên.
- Viết lốt phẩy sinh hoạt hiệu thẳng cột với những dấu phẩy của số bị trừ và số trừ.

6.3. Phép nhân những số thập phân
a) Nhân một số thập phân với một trong những tự nhiên
Muốn nhân một trong những thập phân với một số trong những tự nhiên ta là như sau:
+ Nhân như nhân những số từ bỏ nhiên
+ Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi sử dụng dấu phẩy bóc ở tích ra bấy nhiêu chữ số tính từ lúc phải thanh lịch trái.

b) Nhân một số thập phân cùng với 10, 100, 1000,…
Muốn nhân một số trong những thập phân cùng với 10, 100, 100,… ta chỉ vấn đề chuyển lốt phẩy của số đó lần lượt sang trọng bên bắt buộc một, hai, ba,… chữ số.
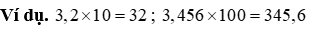
c) Nhân một trong những thập phân với một vài thập phân
Muốn nhân một trong những thập phân với một số thập phân ta làm như sau:
+ tiến hành phép nhân như nhân các số từ bỏ nhiên
+ Đếm xem trong phần thập phân của tất cả hai vượt số có bao nhiêu chữ số rồi dùng dấu phẩy bóc tách ở tích ra từng ấy chữ số tính từ lúc phải lịch sự trái

(hai thừa số có tất cả ba chữ số ở phần thập phân, ta dùng dấu phẩy tách ở tích ra tía chữ số tính từ lúc trái sang trọng phải)
d) Nhân một số thập phân với 0,1; 0,01; 0,001;…
Muốn nhân một trong những thập phân cùng với 0,1; 0,01; 0,001;… ta chỉ bài toán chuyển lốt phẩy của số kia lần lượt sang bên trái một, hai, ba,… chữ số.
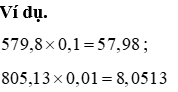
6.4. đặc thù của phép nhân

6.5. Phép chia những số thập phân
a) Chia một trong những thập phân cho một vài tự nhiên
Muốn chia một vài thập phân cho một vài tự nhiên ta làm cho như sau:
- phân tách phần nguyên của số bị chia cho số chia.
- Viết vệt phẩy vào bên buộc phải thương đã tìm được trước khi đem chữ số thứ nhất ở phần thập phân của số bị phân tách đẻ thực hiện phép chia.
- liên tiếp chia cùng với từng chữ số thập phân của số bị chia.
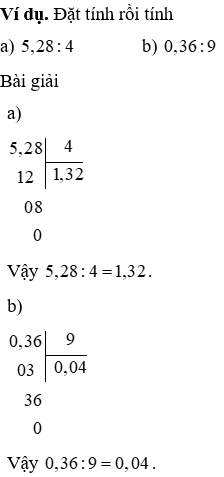
b) Chia một vài thập phân mang lại 10, 100, 1000,…
Muốn chia một số trong những thập phân mang đến 10, 100, 1000,… ta chỉ bài toán chuyển lốt phẩy của số đó lần lượt sang phía bên trái một, hai, ba,… chữ số.
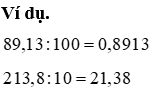
c) Chia một vài tự nhiên cho một vài tự nhiên mà lại thương tìm được là một vài thập phân
Khi chia một số trong những tự nhiên cho một trong những tự nhiên ngoài ra dư, ta thường xuyên chia như sau:
+ Viết vệt phẩy vào bên bắt buộc số thương.
+ hiểu biết thêm vào bên cần số dư một chữ số 0 rồi chia tiếp.
+ nếu như còn dư nữa, ta lại viết cung ứng bên yêu cầu số dư new một chữ số 0 rồi tiếp tục chia, và hoàn toàn có thể cứ làm như thế mãi.
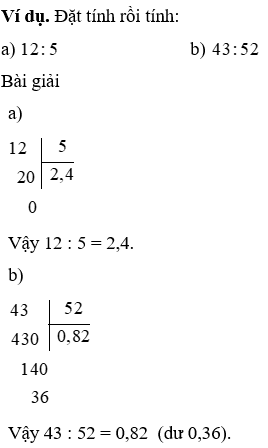
d) Chia một số trong những tự nhiên cho một số thập phân
Muốn chia một số tự nhiên cho một vài thập phân ta làm như sau:
- Đếm xem gồm bao nhiêu chữ số ở vị trí thập phân của số phân tách thì viết thêm vào bên đề nghị số bị chia bấy nhiêu chữ số 0.
- bỏ dấu phẩy sống số phân chia rồi triển khai phép phân chia như chia những số trường đoản cú nhiên.

e) Chia một số thập phân mang đến 0,1; 0,01; 0,001…
Muốn chia một vài thập phân đến 0,1; 0,01; 0,001… ta chỉ vấn đề chuyển dấu phẩy của số đó lần lượt sang trọng bên phải một, hai, ba,… chữ số.

f) Chia một vài thập phân cho một vài thập phân
Muốn chia một số thập phân cho một thập phân ta có tác dụng như sau:
+ Đếm xem gồm bao nhiêu chữ số ở vị trí thập phân của số phân chia thì gửi dấu phẩy sống số bị phân tách sang bên buộc phải bấy nhiêu chữ số.
+ bỏ dấu phẩy nghỉ ngơi số phân chia rồi triển khai phép phân chia như chia cho số từ nhiên.

TỈ SỐ PHẦN TRĂM
1. Tư tưởng Tỉ số phần trăm
có thể viết bên dưới dạng là a%, tuyệt = a%
+ Tỉ số phần trăm là tỉ số của nhì số mà trong những số ấy ta đưa mẫu của tỉ số về 100.
+ Tỉ số phần trăm thường được sử dụng để bộc lộ độ lớn tương đối của một lượng này so với lượng khác.
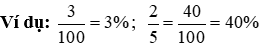
2. Các phép tính với tỉ số phần trăm

3. Những bài toán cơ bản của tỉ số phần trăm
Bài toán 1: tìm tỉ số tỷ lệ của nhì số
Muốn tìm tỉ số phần trăm của nhị số ta làm như sau:
- tìm kiếm thương của nhị số đó dưới dạng số thập phân.
- Nhân thương đó với 100 và viết thêm kí hiệu tỷ lệ (%) vào bên bắt buộc tích kiếm tìm được
Ví dụ: search tỉ số phần trăm của 315 với 600

Bài toán 2: Tìm giá chỉ trị xác suất của một trong những cho trước
Muốn tìm giá trị phần của một trong những cho trước ta đem số đó phân chia cho 100 rồi nhân với số phần trăm hoặc rước số kia nhân cùng với số tỷ lệ rồi chia cho 100.
Ví dụ. ngôi trường Đại Từ có 600 học tập sinh. Số học viên nữ chiếm 45% số học viên toàn trường. Tính số học sinh nữ của trường.

Bài toán 3: search một số, biết cực hiếm một tỉ số xác suất của số đó
Muốn tìm một trong những khi biết giá bán trị xác suất của số đó ta mang giá trị phần trăm của số đó chia cho số tỷ lệ rồi nhân với 100 hoặc ta lấy giá trị tỷ lệ của số kia nhân cùng với 100 rồi phân chia cho số phần trăm.
Ví dụ. Tìm một vài biết 30% của nó bởi 72.

ĐẠI LƯỢNG VÀ ĐO ĐẠI LƯỢNG
1. Bảng đơn vị chức năng đo độ dài
Lớn hơn mét | Mét | Bé rộng mét | ||||
km | hm | dam | m | dm | cm | mm |
1km | 1hm | 1dam | 1m | 1dm | 1cm | 1mm |
= 10hm | = 10dam | = 10m | = 10 dm | = 10cm | = 10mm | |
= km | = hm | = dam | = m | = dm | = mm | |
= 0,1km | = 0,1hm | = 0,1dam | = 0,1m | = 0,1dm | = 0,1mm |
Nhận xét
- Hai đơn vị chức năng đo độ lâu năm liền nhau vội vàng ( hoặc kém) nhau 10 lần.

2. Bảng đơn vị chức năng đo khối lượng
Lớn rộng ki-lô- gam | Ki-lô- gam | Bé rộng ki-lô- gam | ||||
tấn | tạ | yến | kg | hg | dag | g |
1tấn | 1tạ | 1yến | 1kg | 1hg | 1dag | 1g |
=10 tạ | =10 yến | =10kg | =10hg | =10dag | =10g | |
= tấn | = tạ | = yến | = kg | = hg | = dag | |
= 0,1tân | = 0,1tạ | = 0,1yến | = 0,1kg | = 0,1hg | = 0,1dag |
Nhận xét:
- Hai đơn vị đo trọng lượng liền nhau vội (hoặc kém) nhau 10 lần.
- Mỗi đơn vị đo cân nặng ứng với 1 chữ số.
3. Bảng đơn vị đo diện tích s
Lớn rộng mét vuông | Mét vuông | Bé hơn mét vuông | |||||
km2 | hm2 (ha) | dam2 | m2 | dm2 | cm2 | mm2 | |
1km2 | 1hm2 (=1ha) | 1dam2 | 1m2 | 1dm2 | 1cm2 | 1mm2 | |
= 100hm2 = 100 ha | = 100dam2 | = 100m2 | = 100dm2 | = 100cm2 | =100mm2 | ||
= km2 | = hm2 = ha | = dam2 | = m2 | = dm2 | = cm2 | ||
= 0,01km2 | = 0,01hm2 = 0,01 ha | = 0,01dam2 | = 0,01m2 | = 0,01dm2 | = 0,01cm2 |
Nhận xét:
- Hai đơn vị đo diện tích liền nhau vội (hoặc kém) nhau 100 lần.

4. Bảng đơn vị chức năng đo thể tích
Mét khối | Đề - xi -mét khối | Xăng- ti- mét khối |
1m3 | 1dm3 | 1cm3 |
= 1000 dm3 | = 1000 cm3 | |
= m3 | = dm3 | |
= 0,001m3 | = 0,001dm3 |
Nhận xét:
- Hai đơn vị chức năng đo thể tích ngay tức thì nhau vội vàng (hoặc kém) nhau 1000 lần.

HÌNH TAM GIÁC
1. Hình tam giác
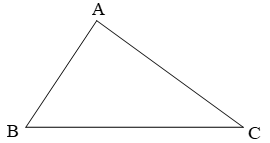
Hình tam giác ABC có:
- Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.
- tía đỉnh là: đỉnh A, đỉnh B, đỉnh C.
- Ba góc là:
Góc đỉnh A, cạnh AB với AC (gọi tắt là góc A);
Góc đỉnh B, cạnh tía và BC (gọi tắt là góc B);
Góc đỉnh C, cạnh AC cùng CB (gọi tắt là góc C).
Vậy hình tam giác bao gồm 3 cạnh, 3 góc, 3 đỉnh.
2. Một số loại hình tam giác
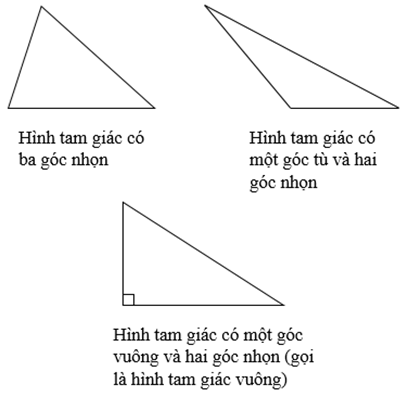
Có 3 mô hình tam giác:
- Hình tam giác có ba góc nhọn
- Hình tam giác tất cả một góc tù với hai góc nhọn
- Hình tam giác có một góc vuông cùng hai góc nhọn (gọi là hình tam giác vuông)
*) mẫu vẽ minh họa
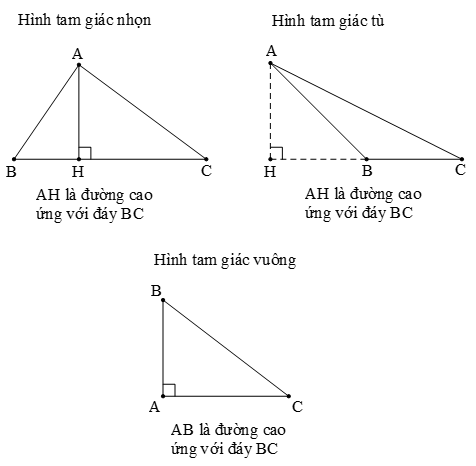
3. Cách khẳng định đáy và mặt đường cao của hình tam giác
4. Diện tích hình tam giác
Quy tắc: ao ước tính diện tích s hình tam giác ta rước độ dài đáy nhân với độ cao (cùng một đơn vị chức năng đo) rồi phân tách cho 2.
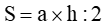
Ví dụ. Tính diện tích s hình tam giác bao gồm độ dài đáy là 13cm và độ cao là 4cm.

HÌNH THANG
1. Định nghĩa: Hình thang tất cả một cặp cạnh đối diện tuy nhiên song.
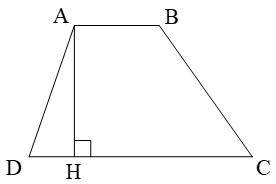
Hình thang ABCD có:
● Cạnh đáy AB cùng cạnh đáy DC. ở bên cạnh AD và sát bên BC.
● AB tuy vậy song cùng với DC.
● AH là con đường cao, độ dài AH là độ cao
*) Hình thang vuông:
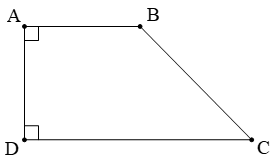
AD vuông góc với hai lòng AB, DC.
AD là mặt đường cao của hình thang của ABCD.
2. Diện tích s hình thang: mong tính diện tích s hình thang ta mang tổng độ lâu năm hai lòng nhân với độ cao (cùng đơn vị chức năng đo) rồi chia cho 2.
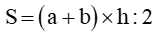
Trong đó:
● a là lòng nhỏ
● b là lòng lớn
● h là chiều cao
Ví dụ. Tính diện tích hình thang biết độ lâu năm hai đáy lần lượt là , và chiều cao .

HÌNH TRÒN
1. Hình tròn. Đường tròn.
Xem thêm: Ông trời mới cult - phim huyền thoại của tương lai (phần 3) vietsub
Vẽ con đường tròn trung ương O, những điểm A, điểm B, điểm M, điểm C nằm trên đường tròn.
-->