Sau những câu hỏi trên lớp hay những bài tập đã làm được thầy cô giáo đào tạo và giảng dạy trên lớp, trên trường, liệu tất cả bài toán khó khăn nhất ráng giới nào cơ mà bạn chưa được biết? Hãy cùng khám phá xem đâu là những câu hỏi khó nhất nhân loại để bạn cũng có thể biết thêm các thông tin có lợi và thú vui hơn nha!
Lịch sử, bắt đầu ra đời của toán học
Rất thọ trước khi lộ diện những văn tự cổ nhất trên nuốm giới, đã có khá nhiều bức vẽ cho biết có một kiến thức và kỹ năng về toán học và biện pháp đo thời gian dựa trên sao trời. Lấy một ví dụ như những nhà cổ sinh vật dụng học đã khám phá ra được những mảnh đất thổ hoàng vào một hang động nằm tại vị trí Nam Phi được tô điểm bởi những hình khắc hình học với thời gian khoảng 70.000 TCN.
Bạn đang xem: Những bài toán hóc búa nhất thế giới
Cũng các di khảo chi phí sử đã có được tìm thấy sinh hoạt châu Phi và nước Pháp, thời gian nằm khoảng chừng giữa 35000 TCN với 20000 TCN, cho biết thêm các nỗ lực sơ khai của tín đồ tiền sử nhằm mục đích định lượng thời gian.
Các vật chứng còn tồn tại cho đến ngày nay đầy đủ thấy việc đếm thời sơ khai công ty yếu là do người phụ nữ, những người giữ những vật ghi lại chu kỳ sinh học của phiên bản thân mặt hàng tháng; ví dụ như hai mươi tám, nhị mươi chín, hoặc ba mươi vạch trên hòn đá hoặc xương rượu cồn vật, theo tiếp đến là một vạch gián đoạn khác. Hơn nữa, những thợ săn thời cổ truyền đã bao gồm khái niệm về một, nhì và các số nữa cũng giống như không lúc chứng kiến tận mắt xét con số cá thể của bè lũ thú.
Xương Ishango được kiếm tìm thấy sinh sống thượng nguồn dòng sông Nile (phía bắc phạm vi hoạt động nước cùng hòa Dân nhà Congo), ở trong thời kì 20.000 TCN. Bạn dạng dịch phổ cập nhất của các hòn đá này cho biết thêm nó là bằng chứng sớm nhất có thể thể hiện tại một dãy những số nguyên tố và phép nhân của ai Cập cổ đại.
Vào thiên niên kỷ thiết bị 5 TCN, bạn Ai Cập cổ kính đã vẽ những bức tranh về xây đắp hình học và không gian. Người ta đã đưa ra các giả thuyết để khẳng định các hòn đá tế thần sinh hoạt Scotland với Anh từ bỏ thiên niên kỷ thiết bị 3 TCN, bao gồm cả các ý tưởng phát minh hình học như hình tròn, hình elip với bộ bố Pythagore trong thi công của nó.
Nền toán học sớm nhất được con người mày mò là sống Ấn Độ cổ kính nằm vào khoảng thời hạn 3000 TCN – 2600 TCN sống nền thanh tao thung lũng Indus (nền tiến bộ Harappa) của Pakistan cùng Bắc Ấn Độ. Nền toán học ở chỗ này đã cách tân và phát triển một khối hệ thống các đơn vị chức năng đo.
Tại Thung lũng Indus cổ điển đã đưa vào và sử dụng hệ cơ số 10, một technology gạch đáng kinh ngạc khi sử dụng các tỉ lệ, những đường đi được bỏ lên một góc vuông cực kì hoàn hảo. Đồng thời một số các hình hình học và thiết kế, bao hàm hình vỏ hộp chữ nhật, thùng phi, hình trụ, hình nón và các bức vẽ minh họa các hình trụ và hình tam giác cắt nhau cùng đồng quy.
Các nguyên tắc dùng vào toán học do những nhà khảo cổ học tìm được gồm 1 thước đo cơ số 10 cùng với độ chia bé dại và cực kì chính xác. Đi kèm cùng với đó là một trong dụng nạm vỏ sò được chuyển động như một loại com pa nhằm đo góc trên mặt phẳng hoặc theo các bội của góc 40 – 360 độ và một dụng cụ vỏ sò khác nhằm đo 8-12 phần của mặt đường chân trời và bầu trời. Tiếp đó là một trong những bộ hiện tượng để đo vị trí của những sao, những hình tinh nhằm mục đích mục đích định hướng. Phiên bản viết tay của fan Indus vẫn chưa được giải nghĩa; vị đó họ biết được siêu ít về các dạng viết của toán học tập Harappan.
Các dẫn chứng khảo cổ sẽ làm nhiều nhà sử học tập trên thế giới tin rằng nền đương đại này đã thực hiện được hệ đếm cơ số 8 cùng đạt được những thành trái về kỹ năng và kiến thức tính tỉ lệ thân chu vi của mặt đường tròn so với bán kính của nó, do đó mà tính được số π chính xác nhất.
6 bài toán khó độc nhất vô nhị trên thế giới được con bạn biết đến
Cộng đồng mạng từng chuyển ra các tranh luận sôi sục về những bài bác toán khi xem qua tưởng như rất đơn giản của học sinh, tuy thế trên thực tiễn lại làm người ta nhức đầu.
Bài toán tuổi đời 263 năm không tìm ra lời giải

Trong nghành toán học, bài bác tập về các số nguyên tố luôn luôn giữ mức độ cực nhọc kỉ lục tốt nhất điển trong khi bài toán về giả thuyết của phòng toán học Christian Goldbach đã làm qua suốt 263 năm tuy vậy vẫn chưa có một ai minh chứng thành công được câu hỏi đó. Bài toán này cũng khá được liệt vào trong những danh sách câu hỏi khó nhất chũm giới.
Năm 1742, trong một bức thư gửi cho đồng nghiệp trên Thụy Sỹ, Goldbach đang đề cập đến những vấn đề liên quan đến thuyết số được phát biểu: “Tất cả các số nguyên khi lớn hơn 2 phần đa là tổng của 3 số nguyên tố”. Chẳng hạn: 35 = 19 + 13 + 3 tuyệt 77 = 53 + 13 + 11.
Sau rộng 250 năm, mọi fan đã thống nhất hotline nó là đưa thuyết Goldbach tam nguyên và có tương đối nhiều nhà toán học dấn thân nghiên cứu núm nhưng cho tới bây giờ thì vẫn chưa tồn tại một ai tìm thấy được đáp án của việc này.
Cho mang đến thời điểm hiện giờ thì bạn được cho là tiếp cận gần nhất với vấn đề này là đơn vị toán học tập Terence Tao đến từ trường đh California làm việc Los Angeles, Mỹ. Nhà toán học tập này đã chứng tỏ được mỗi số lẻ là tổng về tối đa 5 số nguyên tố và hi vọng là phiên bản thân có thể giảm trường đoản cú 5 xuống còn 3 để sở hữu được thắng lợi tuyệt đối trước trả thuyết Goldbach sau này không xa.
Bài toán dễ dàng và đơn giản “Ai giữ lại cá” tuy thế khiến không ít người đề xuất chào chiến bại trước Albert Einstein.

Vào cuối thay kỉ XIX, nhà bác bỏ học nổi tiếng người Đức Albert Einstein đã giới thiệu một câu đố cùng ông quả quyết chỉ bao gồm rất ít tín đồ trên quả đât là rất có thể giải được bài toán này!
Đề bài toán:
Có 5 ngôi nhà, mỗi căn nhà được sơn bởi một màu không giống nhau.
Chủ nhân của mỗi khu nhà ở này lại mang trong mình một quốc tịch khác nhau.
5 người sở hữu của nơi ở này thì mỗi cá nhân lại chỉ mê say một loại nước uống, hút một hãng thuốc lá khác nhau và nuôi một loài vật nuôi riêng.
Không tất cả vị người chủ sở hữu nào lại ưa thích uống cùng một một số loại nước uống, hút và một hãng dung dịch lá và bao gồm cùng một sinh vật nuôi.
Bài toán khôn xiết hóc búa nhưng mà chỉ 0,001% bạn giải được
Bài toán cực kỳ hóc búa này được xếp thứ hạng là trong những bài toán cạnh tranh nhất thế giới. đầu tiên tiên, việc này được chuyển vào trong kỳ thi SAT năm 1982 với chỉ tất cả 3 trong tổng thể 300.000 thí sinh tham gia đưa ra câu vấn đáp chính xác.

Đề bài: Cho cung cấp kính hình tròn B cấp 3 lần chiều dài chào bán kính hình trụ A. Nếu hình trụ A lăn xung quanh hình tròn trụ B thì nó phải thực hiện bao nhiêu vòng quay để có thể trở lại điểm xuất phát?
=> các phương án được chuyển ra khiến cho thí sinh chọn lựa là 3/2, 3, 6, 9/2, 9 vòng.
Cả đa phần thí sinh dự kỳ thi SAT năm đó và không ít người khi đọc đề thi này mọi chọn phương án số 3 là câu vấn đáp đúng.
Tuy nhiên, nếu mang hệ quy chiếu là vòng tròn A thì nó chỉ tự xoay quanh 3 vòng. Thế nhưng nếu lấy hệ quy chiếu không nằm bên trên vòng A thì nó đang quay được 4 vòng, vòng thiết bị tư chính là do vòng tròn B tặng kèm thêm.
Bài toán tra cứu sinh nhật của Cheryl tới từ Singapore

Đề bài:
Bernard cùng Albert vừa kết các bạn với Cheryl. Xem ngày sinh nhật của Cheryl. Sau đó, Cheryl đã giới thiệu 10 đáp án: Ngày 15/5, ngày 16/5, ngày 19/5, ngày 17/6, ngày 18/6, ngày 16/7, ngày 14/7, ngày 14/8, ngày 15/8 và ở đầu cuối là ngày 17/8. Sau đó, Cheryl đã bật mý riêng cùng với Albert cùng Bernard về tháng và ngày sinh của bạn dạng thân mình.
Albert: “Tớ lần khần ngày sinh của Cheryl, mà lại tớ biết có thể Bernard cũng không biết”.
Bernard: “Trước tớ cũng lần chần ngày sinh của chúng ta ấy mà lại giờ tớ biết rồi”.
Albert: “Vậy tớ đã biết ngày sinh nhật thật sự của Cheryl”.
Vậy theo những bạn, Cheryl sinh ngày nào? Ngay sau khi Alex Bellos đăng vấn đề này lên The Guardian, hàng ngàn người đã bắt đầu đi tra cứu kiếm đáp án. Bình luận được những người chăm chú nhiều nhất vẫn thuộc về fan hâm mộ Colinus với câu hỏi thể hiện sự bất lực của anh ý trước vấn đề đáng lẽ chỉ giành cho học sinh 14-15 tuổi: “Tại sao Cheryl không nói thẳng ra luôn luôn sinh nhật của cô ý ấy mang lại hai bạn?”.
Đây là một thắc mắc có vào đề thi của cuộc thi Olympic Toán học châu Á năm 2015, theo Mothership.sg. Thực ra, người ra đề chỉ hy vọng kiểm tra tài năng suy luận của thí sinh tham gia chứ không phải kĩ năng làm toán của họ.
Và đáp án chính xác là sinh nhật của Cheryl là ngày 16/7 (July 16).
Bài toán tra cứu số áo của Mỹ năm 2014

Đây là câu hỏi được chỉ dẫn trong cuộc thi Toán đất nước mỹ năm 2014.
Đề bài:
Có tía thành viên trong đội bóng chày cô bé trường trung học tập Euclid đang nói chuyện với nhau.
Ashley: Tớ vừa phân biệt số áo của 3 bầy mình đa số là số nguyên tố tất cả hai chữ số.
Bethany: Tổng hai số áo của chúng ta chính là ngày sinh của tớ vừa diễn ra trong tháng này.
Caitlin: Ừ, vui thật, thật trùng thích hợp khi tổng nhì số áo của những cậu lại là thiết yếu ngày sinh của tớ vào vào cuối tháng này.
Ashley: với tổng số áo của cả hai cậu lại bằng đúng ngày hôm nay.
Vậy vào đội, Caitlin khoác áo số mấy?
(A) 13 (B) 11 (C) 17 (D) 19
Đây là một trong bài toán tương đối thú vị cùng cũng không quá khó nhằm giải. Cũng chính vì tất cả các ngày được kể tới trong câu chuyện đều phía trong cùng một tháng, đề xuất ngày sinh của Caitlin là phệ nhất, tức là bằng 30, ngày bây giờ là ngày 28 và ngày sinh của Bethany là 24. Từ bỏ đó thuận lợi tìm được số áo của Ashley đó là 13, của Bethany là 17 cùng còn Caitlin với áo số 11.
Bài toán về hiệp sĩ cùng kẻ giả dối của Liên Bang Nga
Những dạng bài toán về hiệp sĩ khôn cùng được mến mộ ở nước Nga. Vào một kỳ thi Olympic dành riêng cho những học viên lớp 9, người ra đề đã chỉ dẫn một bài xích toán cực kỳ thú vị.
Cho 30 tín đồ ngồi quanh một bàn tròn có 30 dòng ghế được đặt số theo thứ tự từ là 1 đến 10. Một số trong số chúng ta là hiệp sĩ, một số lại là người lừa dối. Hiệp sĩ luôn luôn nói thật còn hồ hết kẻ lừa dối thì luôn nói dối. Mọi cá nhân chỉ gồm đúng một tín đồ bạn trong những những bạn khác.
Hơn nữa, người bạn của hiệp sĩ lại là người lừa dối và chúng ta của kẻ lừa dối lại là hiệp sĩ. Mọi cá nhân sẽ phần đông được hỏi: “Có phải bạn của anh sẽ ngồi cạnh bên anh không?” 15 tín đồ khi ngồi ở trong phần lẻ trả lời: “Đúng”.
Tìm số fan đang ngồi tại đoạn chẵn cũng đưa ra câu trả lời: “Đúng”.
Tiến sĩ trằn Nam Dũng hiện đang là giảng viên Đại học khoa học Tự nhiên, của Đại học giang sơn TP sài gòn đã chuyển ra giải thuật đáp như sau: tự đề bài đã cho, ta có thể suy ra trong 30 người dân có đúng 15 cặp hiệp sĩ với kẻ lừa dối là chúng ta của nhau. Từ bỏ đó, ta có thể dễ dàng suy luận được đáp số của bài toán này bằng cách “giả định” cả 15 người tại phần lẻ hầu hết là hiệp sĩ. Lúc đó, tất nhiên bạn của những hiệp sĩ này gần như ngồi cạnh ở những vị trí chẵn và sẽ đều là người lừa dối, vì đó không người nào nói “Đúng”. Đáp số và đúng là 0.

Tuy nhiên, phía trên chỉ là dự đoán đáp số của việc chứ chưa hẳn lời giải. Với bí quyết hỏi ở đề bài, ta vẫn biết đáp số là 0. Tuy nhiên để xác minh được điều này, ta bắt buộc phải minh chứng chứ phải không chỉ là đưa ra một ví như vậy.
Nếu chúng ta quá sa đà vào vấn đề xét địa chỉ ngồi của toàn bộ 30 tín đồ (ai là hiệp sĩ cùng ai là người nói dối) thì sẽ rất rối cũng chính vì có rất nhiều trường hòa hợp xảy ra. Bí quyết của giải mã ở đây là là ở nhận xét đặc biệt quan trọng sau:
Trong 2 tín đồ là bạn của nhau thì chỉ có đúng 1 tín đồ nói “Đúng” cho thắc mắc “Có phải bạn của anh đã ngồi sát bên anh không?”. Thật vậy, nếu tất cả hai người, 1 hiệp sĩ với 1 kẻ lừa dối là các bạn của nhau. Xét 2 ngôi trường hợp:
Nếu họ ngồi cạnh nhau thì hiệp sĩ sẽ công bố nói đúng, còn kẻ lừa dối vẫn nói “Không”.
Nếu họ không ngồi cạnh nhau thì hiệp sĩ vẫn nói “Không”, còn kẻ lừa dối đã nói “Đúng”.
Như vậy, chính vì ta có 15 cặp bạn bè nên ta sẽ có được đúng 15 câu vấn đáp “Đúng”. Vì cả 15 người tại đoạn lẻ hồ hết đã nói “Đúng” nên tất cả những bạn ngồi tại phần chẵn số đông nói “Không”. Có nghĩa là đáp số của bài bác đưa ra bằng 0.
Vậy nên nội dung bài viết này shop chúng tôi đã cung cấp cho chính mình đọc hồ hết bài toán khó nhất thế giới cũng như giới thiệu cho mình sự ra đời của xuất phát toán học.
Trả lời Hủy
Email của bạn sẽ không được hiển thị công khai. Những trường buộc phải được lưu lại *
Bình luận *
Tên *
Email *
Trang website
lưu giữ tên của tôi, email, và trang web trong trình phê duyệt này cho lần comment kế tiếp của tôi.
Toán là cỗ môn khoa học mang tính ứng dụng cao trong cuộc sống và mãi sau nhiều túng bấn ẩn. Đến nay, những phương trình, đưa thuyết vẫn là thách thức lớn đối với các đơn vị toán học.Bạn đang xem: Những câu hỏi khó nhất trái đất chưa giải được
Vừa qua, giáo sư người Anh Andrew Wiles giành giải thưởng Abel với 700.000 USD nhờ chứng minh được Định luật mập Fermat, phương trình đã thử thách các nhà toán học tập trong rộng 350 năm. Mặc dù nhiên, nghành này vẫn vĩnh cửu nhiều sự việc bí ẩn, chưa xuất hiện lời giải.
Giả thuyết Goldbach tam nguyên
 |
| Goldbach mang đến rằng, tất cả các số nguyên tố lớn hơn 2 là tổng của 3 số nguyên tố. Ảnh minh họa. |
Nó được phát biểu như sau: toàn bộ các số nguyên to hơn 2 hầu hết là tổng của 3 số nguyên tố.
Trong hơn 270 năm qua, bạn tiếp cận gần nhất với giải thuật cho bài toán có vẻ đơn giản dễ dàng này là đơn vị toán học Terence Tao của Đại học California sống Los Angeles, Mỹ.
Ông đã chứng tỏ được mỗi số lẻ là tổng buổi tối đa 5 số nguyên tố và hy vọng có thể giảm từ 5 xuống 3 để “chiến chiến hạ tuyệt đối” mang thuyết Goldbach trong tương lai.
Giáo sư giải phương trình 350 năm dấn thưởng 700.000 USDGiáo sư Andrew Wiles giải phương trình 350 năm vừa giành giải Abel năm 2016 với tiền thưởng 700.000 USD. Phương trình này đã làm nặng nề những bộ não thông minh nhất thế giới. |
Giả thuyết Riemann
Giả thuyết này được Bernhard Riemann chỉ dẫn lần thứ nhất năm 1859. Đây là sự việc toán học sâu sắc, liên quan sự phân bố các số nguyên tố.
Thoạt nhìn bao gồm vẻ những số nguyên tố phân bổ ngẫu nhiên, không theo quy tắc nào, cơ mà nó liên kết chặt chẽ với một hàm số Zeta vì nhà toán học Leonard Euler đưa ra.
Riemann nêu ý tưởng các quý giá không cân xứng với hàm số Euler được sắp xếp theo sản phẩm công nghệ tự. Giả thuyết trên được rất nhiều nhà toán học tập dày công nghiên cứu và tra cứu cách giải quyết và xử lý trong 150 năm qua. Họ đánh giá tính đúng chuẩn của nó trong 1,5 tỷ giá chỉ trị trước tiên nhưng vẫn không minh chứng được.
Các nhà toán học tập coi đây là một một trong những bài toán đặc biệt nhất chưa được giải trong toán học tập thuần túy.
Năm 2000, Viện Toán học Clay ở Mỹ treo giải một triệu USD cho người chứng minh được trả thuyết Riemann. Một nhà kỹ thuật đã giới thiệu lời phản bác bỏ giả thuyết cơ mà không được trao thưởng.
Giả thuyết Hodge
Khoa học của những hình khối và không gian đang dần dần đi tới hình học tập của “tính đồng đẳng”. Giới toán học tạo ra những tiến bộ đáng nhắc trong bài toán phân một số loại toán học. Mặc dù nhiên, việc mở rộng các khái niệm khiến bản chất hình học dần biến mất trong toán.
Năm 1950, công ty toán học người Anh William Hodge nêu mang thuyết trong một số trong những dạng không gian, các thành phần của tính đồng đẳng đã tìm lại bản chất hình học tập của chúng.
Viện Toán học Clay đề ra mức thưởng một triệu USD cho tất cả những người có thể chứng minh hoặc chưng bỏ mang thuyết Hodge. Mặc dù nhiên, mang lại nay, nó vẫn chính là vấn đề túng thiếu ẩn.
Giả thuyết của Birch và Swinnerton-Dyer
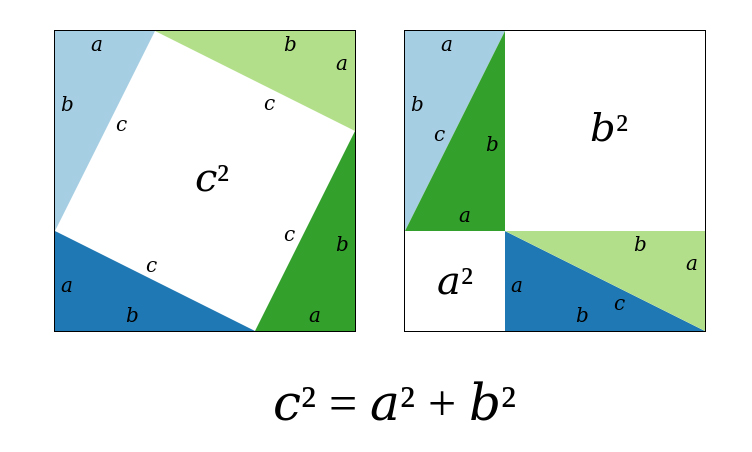
Những số nguyên như thế nào là nghiệm của phương trình x^2 + y^2 = z^2? bao hàm nghiệm hiển nhiên, như 3^2 + 4^2 = 5^2.
Cách trên đây hơn 2.300 năm, Euclide đã chứng tỏ rằng phương trình này còn có vô số nghiệm. Nhưng với các hệ số và số mũ của phương trình phức hợp hơn, sự việc này không hề đơn giản.
Trong vòng rộng 30 năm trở về đây, tín đồ ta phát hiện không có phương pháp chung nào chất nhận được tìm ra số những nghiệm nguyên của phương trình dạng này.
Đầu thập niên 60, so với nhóm phương trình đặc biệt quan trọng nhất gồm đồ thị là những đường cong elip nhiều loại 1, hai nhà toán học fan Anh Bryan Birch và Peter Swinnerton-Dyer sẽ giả thuyết số nghiệm của phương trình phụ thuộc một hàm số f: nếu hàm số f triệt tiêu tại giá trị bằng 1 (nghĩa là giả dụ f(1)= 0), phương trình có vô số nghiệm. Nếu không, số nghiệm là hữu hạn.
Giả thuyết bên trên được tuyên bố một cách đơn giản dễ dàng nhưng nó đã thách thức các bên toán học trong nhiều năm qua.
Vì thế, giải thưởng trị giá một triệu USD vày Viện Toán học tập Clay đề ra vẫn chưa tìm kiếm được chủ nhân.
Bài toán dễ nhưng mà khó: 7 + 2 = ?
Theo Quora, những việc dễ nhưng khó tiếp sau đây không dễ dàng và đơn giản chỉ là những phép tính. Nói yên cầu người giải phải để ý đến kỹ nhằm tìm ra quy luật.
vấn đề Toán học vấn đề Toán học bí ẩn vấn đề Toán học chưa xuất hiện lời giải vấn đề Toán học không được minh chứng giả thuyết Viện Toán học Clay

Đáp án bài toán "chỉ dành cho thiên tài"
3 2 1 30
Đáp án việc mà người đăng lên mạng cho rằng "chỉ dành riêng cho thiên tài" là 98. Nhiều người đưa ra giải pháp 99 tuy vậy không chính xác.

Phép toán vô lý: 1 x 2 = 5
6 5 1 465
Những phép toán vô lý, phức tạp sẽ trở nên dễ dàng hơn nhiều nếu như bạn tìm ra quy luật ẩn dưới chúng.
Xem thêm: Mỹ: 45 Người Mẫu Nữ Khỏa Thân, Thay Đồ Trước Mặt Đàn Ông Ở, Thế Giới Của Người Mẫu Khỏa Thân

vấn đề dễ mà lại khó: 7 + 2 = ?
8 7 1 1121
Theo Quora, những việc dễ nhưng khó tiếp sau đây không đơn giản và dễ dàng chỉ là những phép tính. Nói yên cầu người giải phải lưu ý đến kỹ để tìm ra quy luật.