Hàm số bậc 2 là 1 trong những trong những nội dung thiết yếu cần học tập trong lịch trình môn toán trên THPT. Thâu tóm được tình hình chung của chúng ta học sinh, Monkey sẽ tổng hợp kim chỉ nan và những dạng bài xích tập về hàm số bậc hai, giúp bạn dễ dãi ôn tập cũng giống như ghi ghi nhớ lượng kỹ năng và kiến thức này.
Bạn đang xem: Đồ thị hàm số bậc 2
Ôn tập các kiến thức về hàm số
Trước khi tới với kỹ năng của hàm số bậc 2, Monkey mời chúng ta ôn tập lại các định hướng về hàm con số giác nói phổ biến ngay dưới đây.
Khái niệm hàm số
Nếu đại lượng y dựa vào vào đại lượng biến đổi x, sao cho từng giá trị của x ta luôn khẳng định một giá trị tương tự y, thì y hotline là hàm số của x, với x được hotline là trở nên số của y.
Kí hiệu của hàm số
Hàm số thường được cam kết hiệu bằng các chữ loại như f, g cùng h. Bao gồm dạng như sau: y = f (x) với cách đọc là “y bằng f của x”, trong đó: x là đối số của hàm y = f (x), với y là quý hiếm của hàm y = f (x).
Định nghĩa của hàm số
Cho X, Y là nhị tập hòa hợp số, ví dụ là tập hòa hợp số thực, hàm số f khẳng định trên X, nhận giá trị trong Y là một trong quy tắc cho tương ứng mỗi số x ở trong X với một số trong những y nhất thuộc Y.
Một số tính chất của hàm số
Khi x chuyển đổi mà y luôn luôn nhận một quý hiếm thì y điện thoại tư vấn là hàm hằng.
Hàm số rất có thể biểu diễn bằng bảng, bởi công thức toán học.
Khi y là hàm số của x thì ta tất cả 3 bí quyết viết sau:
f : X → Y
f : x → (x)
y = f(x)
Trong đó:
Tập X call là miền xác định.
Tập Y hotline là miền giá chỉ trị.
x hotline là đối số.
y là một trong hàm số.
f(x) được gọi là cực hiếm của hàm f trên x.
Các dạng hàm số
Hàm số solo ánh: Một hàm số là đối chọi ánh lúc nó vận dụng lên 2 đối số khác nhau luôn mang lại 2 cực hiếm khác nhau. Có nghĩa là với 2 vươn lên là x1 và x2 (x1 # x2) thì f(x1) # f(x2).
Hàm số toàn ánh: Hàm số f được hotline là toàn ánh nếu như với mọi số y ở trong Y ta luôn tìm được ít nhất một số trong những x ở trong X sao để cho f(x) = y tốt y = f(x)
Hàm số song ánh: Trong toán học, tuy vậy ánh, hoặc hàm song ánh, là một trong những hàm số f trường đoản cú tập X vào tập Y vừa lòng tính chất, đối với mỗi y thuộc Y, có duy tuyệt nhất một x thuộc X làm sao để cho f(x) = y.
Hàm số bậc 2 là gì?
Hàm số bậc hai là hàm số có dạng ax^2 + bx + c trong số đó a,b,c là những hằng số cùng (a # 0). Gồm tập xác định D = R và biệt thức = b2 - 4ac. Hệ số hoàn toàn hoàn toàn có thể ở y. Đồng thời, x và y theo thứ tự là các biến.
Trường hợp có 2 vươn lên là x với y, hàm số bao gồm dạng: f(x,y) = ax^2 + by^2 + cxy + dx + ey + f
Một số thuật ngữ bắt buộc nhớ:Hệ số: Hệ số là 1 trong những nhân tử của một biểu thức trong toán học, một giá bán trị cơ mà nó lộ diện phía trước hoặc xuất hiện trong phép nhân với một quý giá khác và thường là một vài nhưng chưa phải biến số.
Bậc của hàm: Thuật ngữ "đa thức bậc hai" đôi khi có nghĩa là "có bậc là 2", hoặc đôi lúc là "có bậc tối đa là 2". Nếu bậc nhỏ tuổi hơn 2, điều này rất có thể được hotline là "trường thích hợp suy biến". Thông thường, nghĩa của thuật ngữ sẽ được khẳng định bởi ngữ cảnh.
Biến: biến chuyển số là một vài có quý hiếm bất kỳ, và tất cả thể biến đổi giá trị vào một tình huống bất kỳ. Một nhiều thức bậc hai có có một biến tuyệt nhất x (trường hợp đối chọi biến), hoặc những như biến hóa x, y, cùng z (trường hợp nhiều biến). Trên thực tế, người ta thường quy một hàm nhiều biến về những hàm 2 vươn lên là để dễ xét.
| ĐỪNG BỎ LỠ!! chương trình học Toán bằng tiếng Anh, giúp cải cách và phát triển tư duy một cách trọn vẹn nhất. Nhấn ưu đãi lên tới 40% ngay TẠI ĐÂY! |
Cách vẽ các dạng vật thị hàm số bậc 2
Đồ thị của hàm số bậc 2 có dạng như vậy nào? Là thắc mắc phổ biến trong những đề thi lớp 9 với lớp 10. Sau đó là cách vẽ những dạng vật thị hàm số bậc nhì mà bạn phải nắm kỹ.
Hàm số bậc hai bao gồm dạng y = ax^2
Các cách vẽ đồ thị:
Bước 1: Xác định tọa độ của đỉnh (0;0)
Bước 2: khẳng định khoảng 5 điểm thuộc trang bị thị để vẽ vật dụng thị đúng chuẩn hơn.
Bước 3: Vẽ parabol
Lưu ý: Khi vẽ parabol cần chú ý đến vết của hệ số a (a > 0 bề lõm tảo lên trên, a điều tra khảo sát hàm số bậc 2
Bảng biến hóa thiên của hàm số y=ax^2+bx+c chia làm 2 ngôi trường hợp:
Trường thích hợp a > 0, hàm số nghịch biến hóa trên khoảng (−∞ ; −b/2a) với đồng vươn lên là trên khoảng (−b/2a ; +∞).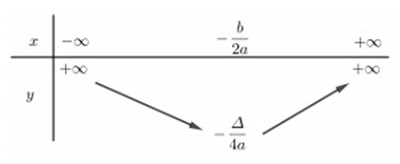
I = (-b2a;-∆4a)Bước 2: Xác định trục đối xứng x = (-b)/(2a) với hướng bề lõm của parabol.Bước 3: Xác định một số điểm ví dụ của parabol (chẳng hạn, giao điểm của parabol với những trục toạ độ và những điểm đối xứng với chúng qua trục trục đối xứng).Bước 4: Căn cứ vào tính đối xứng, bề lõm và dáng vẻ parabol để vẽ parabol.
Monkey Math - học tập Toán theo chương trình GDPT bắt đầu cho trẻ Mầm non & Tiểu học
Tổng hợp toàn bộ các kiến thức và kỹ năng về hàm số số 1 và dạng bài xích tập thường gặp
Chi tiết lý thuyết và bài xích tập áp dụng hàm con số giác, phương trình hàm số lượng giác vào toán học
Khảo giáp sự thay đổi thiên của hàm số bậc 2
Hàm số bậc 2 đồng biến khi nào?
Hàm số f(x) được gọi là đồng vươn lên là trên K (K là một trong những khoảng, một đoạn hay nửa đoạn), đối với mỗi cặp x1, x2 ở trong K nhưng x1
Cho hàm số y = f(x) bao gồm đạo hàm f’(x) trên K. Nếu f’(x) >= 0, với tất cả x ở trong K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) đồng biến.
Hàm số bậc 2 nghịch trở thành khi nào?
Hàm số f(x) được gọi là nghịch đổi thay trên K (K là 1 khoảng, một đoạn xuất xắc nửa đoạn), nếu như với mỗi cặp x1, x2 ở trong K nhưng x1 f(x2).
Cho hàm số y = f(x) bao gồm đạo hàm f’(x) trên K. Nếu như f’(x) =
Cực trị của hàm số bậc nhị là gì?
Lý thuyết về cực trị của hàm số bậc hai:

Cách lập bảng phát triển thành thiên của hàm số bậc hai
Bước 1: tìm kiếm tập xác định.
Bước 2: Tính y′. Tìm những điểm tại kia y′ bởi 0 hoặc ko xác định.
Bước 3: Lập bảng vươn lên là thiên. Từ bỏ bảng thay đổi thiên đúc rút kết luận.

Một số dạng bài bác tập hàm số bậc 2 thường xuyên gặp
Trong công tác toán học và các đề thi phồ thông, các bạn học sinh đang thường gặp gỡ một số dạng bài tập về hàm số bậc 2 bên dưới đây:
Dạng 1: xác định hàm số bậc hai dạng y = ax^2 + bx +c
Bước 1: Gọi hàm số bậc hai yêu cầu tìm tất cả dạng y = ax^2 + bx + c (a ≠ 0)
Bước 2: Dựa vào giả thiết vào đề bài để tùy chỉnh thiết lập những mối đối sánh và tiến hành giải hệ phương trình với những ẩn a, b, c.
Bước 3: Suy ra hàm số buộc phải tìm.
Dạng 2: Lập bảng vươn lên là thiên với vẽ đồ dùng thị hàm số
Sau khi lập bảng đổi mới thiên, thì nhằm vẽ đồ dùng thị hàm số y = ax^2 + bx + c (a ≠ 0) ta hoàn toàn có thể thực hiện nay theo công việc sau:
Bước 1: Tìm tọa độ đỉnh I
Bước 2: search trục đối xứng của vật thị
Bước 3: Tùy đề bài mà tiếp tục tìm tung độ, hoành độ của vật thị đang cho
Bước 4: Tiến hành vẽ vật dụng thị theo những điểm vẫn xác định
Dạng 3: Tìm giá trị cực đại và quý hiếm cực đái của hàm số
Đây là dạng toán mà bạn phải dựa theo trang bị thị hoặc bảng vươn lên là thiên của hàm số y = ax^2 + bx + c (a ≠ 0) đã mang lại mà xác định điểm cực lớn (max) cùng điểm rất tiểu (min) trong vòng giá trị
Dạng 4: tra cứu tọa độ giao điểm
Để giải được bài toán tìm tọa độ giao điểm của hai đồ thị f(x) cùng g(x), ta cần:
Giải phương trình hoành độ giao điểm f(x) = g(x) (1)Trường vừa lòng (1) tất cả n nghiệm thì hai trang bị thị có n điểm chungGhi chú: Để tìm tung độ giao điểm, cụ nghiệm x vào y = f(x) hoặc y = g(x) để tính y.
Để làm rõ hơn về các dạng bài tập hàm số bậc 2 bên trên đây, mời các bạn đến với phần bài tập có giải mã ngay bên dưới đây.
Một số bài bác tập khẳng định hàm số bậc 2 bao gồm lời giải
Dưới đấy là một số bài toán xác minh hàm số bậc 2 có lời giải chi tiết, được Monkey chọn lọc và tổng hợp. Và đó cũng là các dạng việc thường mở ra trong các đề thi lớp 9 cùng lớp 10, tương tự như kỳ thi thpt Toàn Quốc hằng năm.

Ngoài ra, để xây dựng căn nguyên toán học kiên cố cho trẻ, chúng ta cũng có thể tham khảo ngay vận dụng học toán bằng tiếng Anh Monkey Math giành cho trẻ từ thiếu nhi đến không còn tiểu học. Không chỉ cung cấp các kiến thức toán học chuẩn thuộc chương trình giáo dục đào tạo phổ thông bắt đầu nhất, mà lại còn là một nền tảng góp trẻ phát triển kỹ năng ngôn ngữ (tiếng Anh). Ngoài ra, những tính năng như: Trò chơi, bài bác tập xẻ trợ, cách tiến hành học tích cực,... Giúp trẻ tiếp cận mới kiến thức và kỹ năng một cách thoải mái và tự nhiên và hiệu quả nhất.
Để được tư vấn tốt nhất, ba mẹ hãy tương tác Monkey thông qua tổng đài 1900 63 60 52. Hoặc nhằm lại thông tin ngay TẠI ĐÂY để nhận được không ít ưu đãi lên đến mức 40% và hàng vạn tài liệu tiếp thu kiến thức Miễn Phí.

Trên đấy là tất cả văn bản mà Monkey muốn chia sẻ với bạn đọc. Hy vọng rằng với những kỹ năng và kiến thức về hàm số bậc 2 này, để giúp bạn lạc quan hơn trong số kỳ thi sắp tới tới. Hãy theo dõi phân mục “Kiến thức cơ bản” để dấn thêm các thông tin hữu ích tới đây nhé!
| ĐỪNG BỎ LỠ!! công tác học Toán bởi tiếng Anh, giúp phát triển tư duy một cách trọn vẹn nhất. Dấn ưu đãi lên tới 40% ngay lập tức TẠI ĐÂY! |
Trong lịch trình Đại số lớp 10, đồ gia dụng thị hàm số bậc 2 là phần kiến thức rất quan liêu trọng. Trong nội dung bài viết này, docongtuong.edu.vn sẽ reviews tới những em học tập sinh triết lý chung về hàm số bậc 2 trong lịch trình Toán trung học phổ thông lớp 10 cùng với bộ 20 câu hỏi luyện tập lựa chọn lọc.
1. Triết lý chung về hàm số bậc 2 lớp 10
Trước khi tò mò về đồ thị hàm số bậc 2, các em học viên cần nạm vững các kiến thức căn cơ của hàm số bậc nhì như tư tưởng và chiều vươn lên là thiên trước tiên.
1.1. Định nghĩa
Hàm số bậc hai lớp 10 được khái niệm là dạng hàm số có công thức bao quát là $y=ax^2+bx+c$, trong số ấy a,b,c là hằng số cho trước, $a eq 0$.
Tập xác định của hàm số bậc nhì lớp 10 là: $D=mathbbR$
Biệt thức Delta: $Delta =b^2-4ac$
1.2. Chiều đổi thay thiên cùng bảng thay đổi thiên
Xét chiều trở nên thiên cùng bảng phát triển thành thiên là bước rất đặc trưng để vẽ được đồ gia dụng thị hàm số bậc 2. Mang lại hàm số bậc 2 $y=ax^2+bx+c$ cùng với $a>0$, chiều đổi mới thiên của hàm só bậc hai lớp 10 khi đó là:
Đồng đổi thay trên khoảng chừng $(frac-b2a;+infty )$
Nghịch thay đổi trên khoảng $(-infty ;frac-b2a)$
Giá trị rất tiểu của hàm số bậc hai lớp 10 đạt trên $(frac-b2a; frac-Delta 4a)$. Khi đó, giá trị bé dại nhất của hàm số là $frac-Delta 4a$tại $x=frac-b2a$.
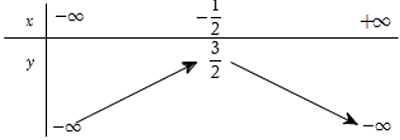
Cho hàm số $y=ax^2+bx+c$ với $a
Đồng phát triển thành trên khoảng $(-infty ;frac-b2a)$
Nghịch biến trên khoảng chừng $(frac-b2a;+infty )$
Giá trị cực đại của hàm số bậc 2 đạt tại $(frac-b2a; frac-Delta 4a)$. Lúc đó giá trị lớn số 1 của hàm số là $frac-Delta 4a$ tại $x=frac-b2a$.
2. Đồ thị hàm số bậc 2 tất cả dạng như thế nào?
2.1. Biện pháp vẽ thứ thị hàm số bậc 2
Để vẽ đồ vật thị hàm số bậc 2, những em học sinh hoàn toàn có thể tuỳ theo từng ngôi trường hợp nhằm sử dụng một trong các 2 phương pháp sau đây.
Cách 1 (cách này có thể dùng cho đầy đủ trường hợp):
Bước 1: Xác định toạ độ đỉnh I
Bước 2: Vẽ trục đối xứng của thứ thị
Bước 3: khẳng định toạ độ những giao điểm của Parabol theo lần lượt với trục tung với trục hoành (nếu có).
Cách 2 (sử dụng bí quyết này khi đồ thị hàm số có dạng $y=ax^2$)
Đồ thị hàm số bậc 2 $y=ax^2+bx+c (a eq 0)$ được suy ra từ thứ thị hàm $y=ax^2$ bằng cách:
Nếu $fracb2a>0$ thì tịnh tiến song song với trục hoành $fracb2a$ đơn vị về phía bên trái, trở về bên cạnh phải giả dụ $fracb2a
Nếu $frac-Delta 4a>0$ thì tịnh tiến tuy nhiên song cùng với trục tung $-left |fracDelta 4a ight |$ đơn vị chức năng lên trên, xuống dưới nếu $frac-Delta 4a
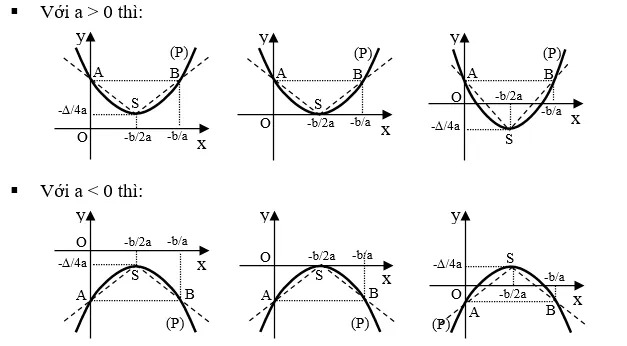
Đồ thị hàm số $y=ax^2+bx+c (a eq 0)$ có dạng như sau:

Đồ thị hàm số bậc nhị lớp 10 $y=ax^2+bx+c (a eq 0)$ có điểm sáng là mặt đường parabol với:
Đỉnh: $I(frac-b2a;frac-Delta 4a)$
Trục đối xứng: đường thẳng $x=frac-b2a$
Nếu $a>0$, phần lõm của parabol quay lên trên; giả dụ $a
Giao điểm với trục tung: $A(0;c)$
Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình $ax^2+bx+c=0$.
Lưu ý: Để vẽ đồ gia dụng thị hàm số bậc 2 đựng trị hoàn hảo và tuyệt vời nhất $y=ax^2+bx+c$ ta làm theo quá trình sau:
Trước không còn ta vẽ đồ dùng thị $(P): ax^2+bx+c$
Ta có:

Vậy vật dụng thị hàm số $y=ax^2+bx+c$ bao hàm 2 phần:
Phần 1: chính là đồ thị hàm số bậc 2 (P) mang phần phái trên trục Ox.
Phần 2: mang đối xứng phần đồ dùng thị (P) bên dưới trục Ox qua trục Ox.
Vẽ đồ gia dụng thị hàm số $(P_1)$ với $(P_2)$, ta được đồ dùng thị hàm số bậc 2 $y=ax^2+bx+c$.
Nắm trọn kiến thức và kỹ năng và phương pháp giải phần đông dạng bài tập Toán thi THPT nước nhà với bộ tài liệu sản phẩm hiếm của docongtuong.edu.vn ngay
2.2. Bài tập lấy ví dụ vẽ trang bị thị hàm số bậc 2
Ví dụ 1: Vẽ thứ thị của hàm số bậc 2$y=x^2+3x+2$
Hướng dẫn giải:
Ta có:

Bảng vươn lên là thiên của hàm số:

Vậy ta có thể suy ra: Đồ thị hàm số $y=x^2+3x+2$có đỉnh I(-3/2;-¼) và đi qua những điểm A(-2;0), B(-1;0), C(0;2), D(-3;2).
Đồ thị hàm số $y=x^2+3x+2$ nhận con đường x=-3/2 làm cho trục đối xứng và có phần lõm phía lên trên.

Ví dụ 2 (Luyện tập 2 trang 41 Toán lớp 10 tập 1): Vẽ vật thị mỗi hàm số bậc nhị sau:
a) $y=x^2–4x–3$
b) $y=x^2+2x+1$
Hướng dẫn giải:
a) $y=x^2–4x–3$
Ta có: $a=1, b=-4, c=-3, =(-4)^2-4.1.(-3)=28$.
Toạ độ đỉnh: I(2;-7)
Trục đối xứng: $x=2$
Giao điểm của parabol cùng với trục tung: A(0;-3)
Giao điểm của parabol với trục hoành: B(2-7;0) và C(2+7;0)
Điểm đối xứng với A(0;-3) qua trục x=2 là D(4;-3)
Vì a>0 phải phần lõm của đồ gia dụng thị hướng lên trên.
Đồ thị của hàm số bậc 2 lớp 10 $y=x^2–4x–3$ gồm dạng như sau:

b) $y=x^2+2x+1$
Ta có: a=1; b=2; c=1; =$2^2-4.1+1=0$
Toạ độ đỉnh: I(-1;0)
Trục đối xứng: x=-1
Giao điểm của parabol cùng với trục tung là A(0;1)
Giao điểm của parabol cùng với trục hoành đó là đỉnh I.
Điểm đối xứng với A(0;1) qua trục đối xứng x=-1 là B(-2;0)
Lấy điểm C(1;4) thuộc thứ thị hàm số đề bài, điểm đối xứng C qua trục x=-1 là vấn đề D(-3;4)
Vì a>0 phải phần lõi của đồ dùng thị hướng lên phía trên.
Đồ thị hàm số $y=x^2+2x+1$ bao gồm dạng sau đây:

Ví dụ 3: Lập bảng trở nên thiên với vẽ đồ vật thị hàm số bậc 2 sau:
$y=x^2-3x+2$
$y=-2x^2+4$
Hướng dẫn giải:
Ta có:

Bảng biến đổi thiên:

Suy ra, trang bị thị hàm số nhận con đường $x=frac32$ làm cho trục đối xứng và tất cả bề lõm hướng lên trên.
Đồ thị hàm số bậc 2 $y=x^2-3x+2$ có mẫu thiết kế như sau:

Ta có:

Bảng thay đổi thiên:

Xét thấy, đồ gia dụng thị hàm số tất cả $y=-2x^2+4x$ nhấn I(1;2) là đỉnh, đi qua những điểm O(0;0), B(2;0).
Suy ra, đồ gia dụng thị hàm số nhận con đường x=1 làm cho trục đối xứng và có bề lõm phía xuống dưới.

3. Rèn luyện vẽ vật thị hàm số bậc 2
Để rèn luyện thành thạo các dạng bài xích tập về đồ thị hàm số bậc 2, những em học sinh cùng docongtuong.edu.vn thực hành thực tế với bộ câu hỏi trắc nghiệm tiếp sau đây nhé!
Câu 1: Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình dưới đây. Xác minh nào sau đó là đúng?

A. $a>0, b
B. $a>0, b0$
C. $a>0, b>0, c>0$
D. $a
Câu 2: Parabol $y=-x^2+2x+3$ tất cả phương trình trục đối xứng là:
A. X=-1
B. X=2
C. X=1
D. X=-2
Câu 3: mang đến hàm số $y=x^2-2x-1$. Mệnh đề như thế nào dưới đó là sai?

Câu 4: Parabol $(P):y=-2x^2-6x+3$ tất cả hoành độ đỉnh bằng bao nhiêu?

Câu 5: Viết phương trình trục đối xứng của đồ dùng thị hàm số bậc 2 $y=x^2-2x+4$

Câu 6: Trục đối xứng của parabol $y=2x^2+2x-1$là đường thẳng bao gồm phương trình:

Câu 7: Toạ độ đỉnh I của parabol $y=x^2-2x+7$ là:

Câu 8: Cho parabol $(P):y=3x^2-2x+1$. Điểm như thế nào sau đây là đỉnh của (P)?

Câu 9: Cho hàm số bậc nhị $y=ax^2+bx+c (a eq 0)$ bao gồm đồ thị hàm số bậc 2 (P), đỉnh của (P) được xác minh bởi bí quyết nào sau đây?

Câu 10: mang đến hàm số $y=ax^2+bx+c (a>0)$. Khẳng định nào sau đấy là sai?

Câu 11: mang lại hàm số $y=(m-1)x^2-2(m-2)x+m-3 (m eq 1)$ (P). Đỉnh của (P) là $S(-1;-2)$ thì m bởi bao nhiêu?

Câu 12: Đồ thị bên dưới là vật dụng thị của hàm số nào?

A.$y=-2x^2+3x-1$
B.$y=-x^2+3x-1$
C.$y=2x^2-3x+1$
D.$y=x^2-3x+1$
Câu 13: Đồ thị hình dưới là đồ dùng thị của hàm số nào?

Câu 14: mang đến hàm số $y=ax^2+bx+c$ tất cả đồ thị như mẫu vẽ sau đây, dấu những hệ số của hàm số đó là:

Câu 15: Hàm số $y=-x^2+2x+3$ tất cả đồ thị là hình nào trong số hình sau đây?

Câu 16:Hàm số nào tiếp sau đây có vật thị như hình?

Câu 17: Hàm số nào tiếp sau đây có vật dụng thị như hình?

Câu 18: Đồ thị hàm số bậc 2: $y=x^2-6x+5$

Đăng cam kết ngay để được các thầy cô hỗ trợ tư vấn và chế tạo lộ trình ôn thi Toán THPT đất nước sớm tức thì từ bây giờ
Câu 19: Hàm số $y=ax^2+bx+c$ gồm đồ thị như hình vẽ sau. Mệnh đề như thế nào dưới đấy là đúng?

Câu 20: Cho vật thị hàm số bậc 2 dạng parabol (P): $y=ax^2+bx+c (a eq 0)$ tất cả đồ thị như hình dưới. Tìm các giá trị m để phương trình $ax^2+bx+c=m$ tất cả 4 nghiệm phân biệt.

Hướng dẫn giải đưa ra tiết
Câu 1:
Chọn A.
Parabol gồm bề lõm quay lên ở trên => $a>0$. Các loại D.
Parabol giảm trục tung trên điểm có tung độ âm phải $c
Câu 2:
Chọn C.
Parabol $y=-x^2+2x+3$ gồm trục đối xứng là con đường thẳng $x=frac-b2a$ => $x=1$.
Câu 3:
Chọn D.
Trục đối xứng của đồ vật thị hàm số là đường thẳng $x=frac-b2a=1$.
Câu 4:
Chọn A
Hoành độ đỉnh của parabol (P) được tính như sau:

Câu 5:
Chọn A.
Đồ thị hàm số $y=ax^2+bx+c$ với $a eq 0$ tất cả trục đối xứng là con đường thẳng có phương trình x=-b/2a
Vậy đồ vật thị hàm số $y=x^2-2x+4$ tất cả trục đối xứng là con đường thẳng phương trình x=1.
Câu 6:
Chọn D.
Phương trình của trục đối xứng là x=-2/2.2=-½
Câu 7:
Chọn B.

Câu 8:
Chọn B.

Câu 9:
Chọn A.
Đỉnh của parabol $(P): ax^2+bx+c (a eq 0)$ là điểm:

Câu 10:
Chọn B.
Dựa bào biến chuyển thiên của hàm số $y=ax^2+bx+c (a>0)$ ta thấy các khẳng định A, C, D đúng.
Khẳng định B là không nên vì bao hàm hàm số bậc nhị không cắt trục hoành như hàm số $y=-2x^2+3x-9/8$
Câu 11:
Chọn A.
Do đỉnh của (P) là S(-1;-2) nên ta có:

Câu 12:
Chọn C.
Đồ thị giảm trục tung trên điểm gồm tung độ bởi 1.
Đồ thị cắt trục hoành tại điểm tất cả hoành độ bằng 1, phương trình hoành độ giao điểm phải có nghiệm x=1, ta tất cả phương trình sau đây:

Câu 13:
Chọn B.
Do bề lõm của đồ gia dụng thị hướng lên trên cần a>0 => một số loại đáp án C, D.
Đồ thị giao trục Ox tại điểm (1;0) và (½; 0) =>
Câu 14:
Chọn B.
Đồ thị là parabol có bề lõm phía xuống dưới yêu cầu $a
Đồ thị giảm chiều dương của trục Oy buộc phải $c>0$.
Trục đối xứng $x=-b/2a>0$, mà $a0$.
Câu 15:
Chọn A.
Do $a=-1$ cần đồ thị tất cả dạng lõm xuống dưới => loại C
Tính toán được đỉnh của đồ gia dụng thị bao gồm toạ độ $I (1;4)$
Câu 16:
Chọn B.
Quan gần cạnh đồ thị ta các loại đáp án A cùng D. Phần trang bị thị bên đề xuất trục tung là đồ dùng thị (P) của hàm số $y=-x^2+5x-3$ cùng với $x>0$, toạ độ đỉnh của (P) là (5/2; 13/4), trục đối xứng là x=2,5. Phần đồ thị bên trái trục tung là vì lấy đối xứng phần thiết bị thị bên yêu cầu của (P) qua trục tung Oy. Ta được cả nhì phần là đồ vật thị của hàm số $y=-x^2+5x-3$.
Câu 17:
Chọn B.
Dựa vào đồ gia dụng thị ta suy được a
$y=-x^2+4x-3 => a=-1; I(2;1)$.
Câu 18:
Chọn D.

Phần vật dụng thị $(C_1)$: là phần đồ vật thị của hàm số $y_1=x^2-6x+5$ nằm cạnh sát phải trục tung.
Phần đồ vật thị $(C_2)$: là phần đô fthij của hàm số $y_2=x^2-6x+5$ bao gồm được bằng cách lấy đối xứng phần đồ dùng thị $(C_1)$ qua trục tung.

Kết luận đồ thị C) bao gồm trục đối xứng phương trình x=0.
Câu 19:
Chọn D.
Quan tiếp giáp đồ thị, ta thấy:
Đồ thị cù bề lõm xuống dưới bắt buộc $a0 b/a $b>0$.
Ta có: Đồ thị cắt Ox tại điểm gồm tung độ âm phải $c
Vậy $a0,c
Câu 20:
Chọn B.
Xem thêm: Top 10 Quà Sinh Nhật Cho Bé Trai 10 Tuổi Giá Tốt T12/2022, Top 10 Quà Tặng Sinh Nhật Cho Bé 7
Quan ngay cạnh đồ thị ta gồm đỉnh của parabol là $I(2;3)$ nên:

Mặt không giống (P) giảm trục tung tại $(0;-1)$ đề nghị $c=-1$. Suy ra:

$(P):y=-x^2+4x-1$ suy ra hàm số $y=-x^2+4x-1$ tất cả đồ thị là phần hình phía trên trục hoành của (P) và phần giành được do mang đối xứng phần dưới trục hoành của (P), như hình vẽ:

Phương trình $ax^2+bx+c=m$ tuyệt $-x^2+4x-1=m$ bao gồm 4 nghiệm phân minh khi mặt đường thẳng $y=m$ cắt đồ thị hàm số bậc 2 $y=-x^2+4x-1$ trên 4 điểm phân biệt.